|
1.
Why do cells divide?
What's
the principle behind this propagation? In
one sense itís like the propagation
of a light beam through
space as it's proposed interpreted
in file EM-waves:
a quantum jump in an atom from a
0-pole completing itself with the
complementary antimatter of "negative"
energy in space to a new 0-pole
and a new quantum jump, as a sine
wave and cosine wave with a displacement
of 90° between magnetic
(M) and electric (E) components: 
Fig
Ge-1-142-2 A cell is
a quantum of energy. DNA resembles
a light beam with its complementary
bases as representing the E- versus
M- factors (a chromosome as a "lumosome").
Like the light
beam the DNA-strands complement
themselves from what is antimatter
on their level in their surrounding,
the manifold of all individual complementary
nucleotides. The
L-type of waves, ←
00í →
0í←
00í →Ö,
could illustrate this factor in
propagation. It seems also expressed
in all building of linear structures
in a cell, proteins, even globular
ones, fatty acid, collagen etc.
Why this rather curious lining up
of the molecules after one another?
"Dipole" bonds are surely
a factor, this concept taken in
a wider sense of some complementary
feature in the individual units
like 0 - 00 in the L-wave.
Elementary
waves as one guiding principle? However,
this feature of propagation is only
a part of an answer. The cell
as a world of trapped motions is
in itself, internally, an ongoing,
repetitive process of breaking-down
and reconstruction as outward and
inward directions in a dimension
chain regarded as a unit. In this
sense the processes get the character
of standing waves. Total
reproductionof a cell from 1
to 2 to 4 ... etc. is certainly
something more.
It's
preceded by a total duplication
of the chromosomes and other organelles
before cell division. Some built-in
program for the step gets activated.
Certain
signals from "anticenter", primary
polarizing force in our model, could
possibly trigger it. Itís said that
in embryological development of
multicellular organisms the first
cell division is initiated from
mothers RNA in cytoplasm, i.e. anticenter
to the nucleus.
Scientists
talk about other conditions, using
concepts as "maturity" and "saturation".
It could point to a correspondence
with processes of crystallization
on the physical level.
Next
part of an answer would be a deeper
polarization, 4 ← 3, from dimension degree (d-degree)
3, the volume that the cell occupies
in a 3-dimensional space, to d-degree
4, this in terms of the dimension
model; the step from inner self-sustaining
("haploid" or partial)
processes to a total duplication
of higher d-degree, including both
DNA strands (double direction, d-degree
4). Through saturation developed
to two separate centers. 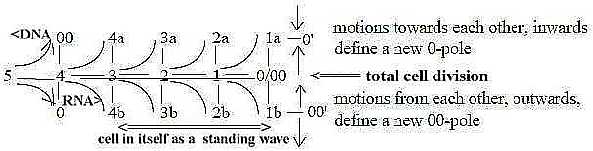
Fig Ge-2-139-1 The step
inwards to d-degree 4 could be seen
expressed by the spindles as opposite,
radial vector fields.
The
centrosomes that seem to guide the
development of these spindles move
also to opposite poles of the nucleus
at start of cell division, i.e.
a polarity of 180°, assumed
in our model as of d-degree 4. (They
are not necessary for cell division
but appear in animal eukaryotes
as substantiations of an underlying
geometry.) Duplication of
haploid chromatids at sexual reproduction
(meiosis) includes over-crossings
with exchange of genes. It has been
said that these over-crossings in
numbers are 1 up to 4 or 5, usually
not more (Bg p. 142).
It sounds astonishing few. Yet,
if the statement is reliable, it
suits well in the dimension model
 Fig
Ge-3-141-4 Fig
Ge-3-141-4 In addition
to the question of why reproduction
it could be said that polarizations
as such is a main principle
in the dimension model. All organism
can also be described as 1/2
on every internal level (see file
Life) as centers in relation
to the surrounding anticenter that
they depend on. ("Saturation"
becomes the expression for this
dependence.).
The inversion of ½
is 2 and in the mathematical depths
of life one could perhaps suspect
a relation between a 4-dimensional
function and its conjugate?
2.
Duplication leading to 2 centers:
If
we imagine the complementary poles
of a dimension chain as nucleotides
of DNA, saturation becomes the completion
from environment as 00-pole with
all its individual nucleotides.
a) Duplication:

Fig
Ge-4-139-1
b) Division,
two "daughter cells": 
Fig
Ge-5-142-1
3.
Do the "daughter cells" become exactly
alike at cell divisions?
The usual answer is yes. However,
the figure above with adding of
"a-and b-poles" to the opposite
strands, the complementary character
of DNA and the opposite directions
of the strands could yet indicate
some underlying difference, at least
at the very creation of two chromosomes?
Following two data point to such
a difference: - Since copying
of the two strands occurs from the
same end but in opposite directions,
copying of one of the strands needs
at least two DNA-polymerase molecules
in a discontinuous operation (Aph
p. 96), while the other is continuously
copied *. 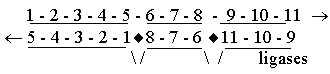 Fig
Ge-6 Fig
Ge-6 *(There
is a similarity in this difference
with the opposition between whole
mRNA chains and the tRNAs with anticodons
representing the other strand. Perhaps
the same principle applied on another
level?) -
The other information: When stem
cells divide, itís said, one of
the daughter cells becomes a stem
cell, the other a functionally specialized
one. In such data it seems
possible to find a first origin
to the later developed sexual differentiation,
a division on different individuals,
characterized by the 0- and 00-poles.
(A
singularity and a multitude, outwards
and inwards.)
4. The
geometrical features at cell division
are really noteworthy and could
support the general hypothesis here
about a geometrical scheme underlying
all manifestations in Nature.
Only
to mention one special thing first:
in the duplication of a centriole
to a pair in a centrosome, the "daughter"
cell, (probably better called son
cell), growths out at straight angle
to the mother cell: a curious fact
that seems hard to explain with
functionality (?). It looks like
an angle step as if it could refer
to the one between the radial spindle
cones that develops from centrosomes
and the equatorial plane of chromosomes?
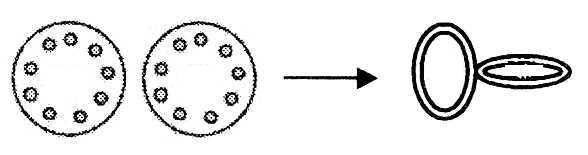
Fig
Ge-7-(139-2)
(The
above mentioned fact that centrosomes
not are necessary organelles for
development of radial spindles at
cell division obviously seems to
underline that the geometries comes
first, as in an architectural drawing,
before their materialization.) Spindles
and equator plain with two sets
of chromosomes: 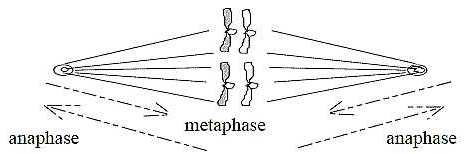 Fig
Ge-8-140-2 This arrangement
can geometrically be seen developed
from the opposite ends of a dimension
chain: 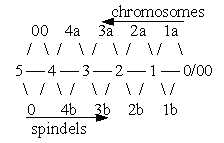 Fig
Ge-9 Fig
Ge-9 a. The linear chromatids
line up and get copied with homologues
paired, d-degree 1 in macro-shape:
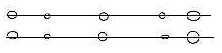 Fig
Ge-10-141-3 Fig
Ge-10-141-3 These pairs
of chromatids get spiraled (a 3-dimensional
motions in d-degree 2) in several
steps, as a kind of substantiation
and contracted to pairs of chromosomes.
They get arranged
in the equator plate (d-degree 2).
Cf. circular geometry of pole 3a
in the model. Chromosomes in anticenter
position here. b. The spindles
develop from centers as the 0-pole
to vector field outwards, pole 4b,
as structures appearing as the radial
pole 3b in the dimension chain.
The
outgrowth of the spindles and then
the pull of chromosomes in anaphase
towards centrosomes imply two phases
of d-degree 4, vectors of outward
(4b) and inward (4a) directions
(outer poles of d-degree 3 in the
dimension chain). The
centromeres are
the ring-formed protein structures
that in some unknown way enclose
and bind the chromosome pairs and
with help of other proteins (kinetochores)
get attached to the spindle threads.
They appear as anticenters in terms
of the dimension chain.
(The fact that itís a meeting between
to radial cones that here "define"
the equator plane as a surface -
or rather a double surface, and
not complementary 3a-3b-poles, shows
that a doubled center (0-poles of
d-degree 4) already is defined.)
The whole process
with regard to the geometrical macro-shapes
in d-degrees:
 Fig
Ge-11-140-1
With
the loop version of the dimension
model we have a meeting of directions
outwards /
inwards in d-degree step 3 - 2,
here between spindles and equatorial
plane with chromosomes. Loop
model: A sketch on the counter directed
processes in first phases: 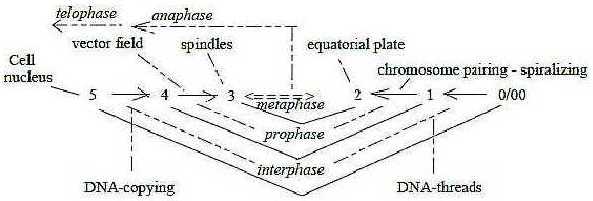
Fig
Ge-12-141-1
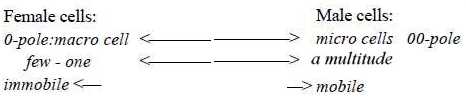
5.
Cell divisions to haploid mail and
female gametes:
Motional
moments increasing towards lower
d-degrees according to the model.
Fig
Ge-13-142-3 -
Female cell: unequal cell divisions
in complementary poles from
higher d-degree outwards, as in
a dimension chain step 4 →>
1 + 3 in numbers. The small cells,
called polar bodies, may indeed
represent virtual male cells. They
"degenerate", which could
be suspected as a description of
how the 00-pole of d-degree 4 gets
debranched and (as through another
dimension) meets the other way around
as pollen. (There is the appearance
of 3 polar bodies, two sets of them,
in ovulum of higher plants.) -
Mail cell: equivalent divisions
20 →>
21 →>
22... as
in a dimension chain from lower
d-degrees inwards, with 2 as log-base.
Cf. increasing motions at lower
d-degrees and tail of the sperm. 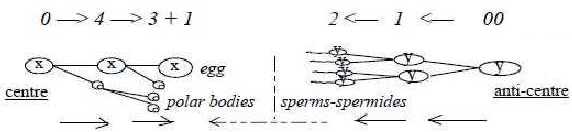
Fig
Ge-14-142-4 (About
egg divisions after fertilization:
3 divisions can be done symmetrical.
Itís said (old information) that
these 8 cells all can develop to
whole individuals. If so, it could
probably or somehow depend on the
fact that 8 quadrants all have direct
contact with origin in a 3-dimensional
coordinate system?)
|


 Fig
Ge-3-141-4
Fig
Ge-3-141-4

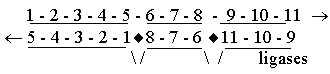 Fig
Ge-6
Fig
Ge-6

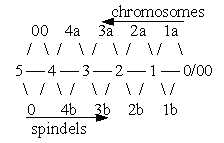 Fig
Ge-9
Fig
Ge-9 Fig
Ge-10-141-3
Fig
Ge-10-141-3


