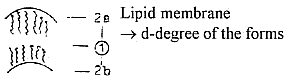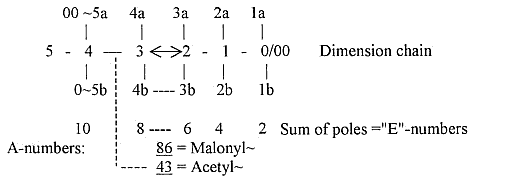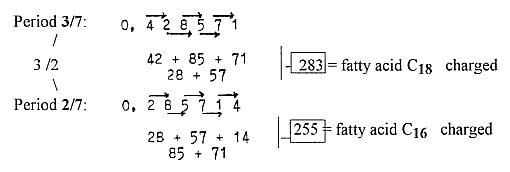| Physics / An elementary 5-dimensional model applied in different sciences |
|
Astronomy
- links:
|
Elements - links:
|
The Genetic Code -
links:
|
Language - links
|
|
The
String Theory - comparisons
|
|
This file as pdf here. When the 5-dimensional model here was developed and the booklet
series behind this home page made publicly available in 2000,
this String Theory (ST) was unknown to me. 1. The level of analysis is optional:
Physicists got problems with infinities appearing in their equations
during the development of quantum physics, where they thought
they had to handle elementary particles as points, and especially
so when trying to unite the general relativity theory for gravitation
with quantum mechanics. This is said to be the background to the
String theory, the motivation to start with 1-dimensional strings
instead of particles as points.
Definition of infinity as anticenter demands of
course a center, a singularity (with physicists' term).
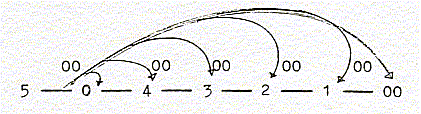
Mathematically, we could think of inversions around number 1 in a coordinate system. To reach the point from number 1 we need to write 10-00. Inverted we get the infinity 10+00. When physicists get infinities in their equations, such as a
probability higher than 1, (in ordinary mathematics impossible)
- we must presume that that there is something wrong, not with
the infinity but with the concept of probability in this Schrödinger
context. Perhaps the error could be found in the attempt to analyze
or find the electrons in two different d-degrees of appearance
at the same time, in the same equations? (As Greene touches upon, the difficulties may have raised through assumptions, which the physicists themselves have invented.) Here we suggest the more general view that these difficult infinities just mean "on the other side of", that a term from the complementary world has been involved in he equations. We could eventually take the footprints of a walking person as an elementary metaphor: the right foot on the ground, with a definite position, the left one up in the "infinity", unspecified, undetermined. (?) Concerning the infinities appearing when physicists try to unite
the gravitational
force
with quantum mechanics: they seem very natural
according to our 5-dimensional model here: this force seen as
defined by direction inwards in d-degree 4 with "outer poles"
00 <=====> 0: When physicists treat particles as points and are confronted
with infinities as problems, we could from our point of view conclude
that they have missed the 5th dimension degree as defined in our
model - or just haven't developed any mathematical way to handle
the 00-pole. In any case, irrespective of the infinity problems, an analysis in d-degree 1 should be as well justified as in terms of 2-dimensional shells or 3-dimensional bodies or vector fields.
The String theory counts with 11 dimensions, the 4 usual ones
with 3 space dimensions plus 1 for Time, and 7 "undeveloped"
ones. In our 5-dimensional model we could imagine the 11 dimensions derived in different ways: a) 10 dimensions (without Time) in some way expressions for the
sum of "outer poles" in d-degree 4 (re-identified as
Direction), what we have called the "E-number". The number 10 then transformed to 4 + 3 + 2 + 1 through d-degree steps, values of the half axes; the other branch of half axes then ignored, connected with E = -mc2 ? b) An addition in a cumulative way ?: With the view of debranched d-degrees in first steps, we get 10 → 8 + 2, → 6 + 4 in sums of poles. In our model we have assumed the
external motions to be just 4-dimensional
in d-degree 1. But this refers to another concept or definition
of dimensions than in the String theory. Since each d-degree of structure in our model principally is possible to analyze in pure motions, according to our postulates, it seems quite compatible with the reference to the "E-numbers" here, the sums of poles in different d-degrees - and with the general view in the String theory. In ST, properties as Mass and Charge are identified as different vibration patterns. (Unfortunately hardly anything more is said about that subject in the reference.)
The ST physicists are looking inwards in the sense inwards towards
Microcosm. As they in several respects, from our point of view,
seem to study our dimension chain from 0/00 inwards *. We could
identify their dimensions as characterized by direction inwards,
but only in this sense. * About the division 4 - 7 and outwards - inwards: Compare
the "mad" idea about "quark-numbers"
in our model in connection with amino
acids: a number + 2 times the mirrored number, sum
divided by 3 etc., the same operation repeated, give chains
of numbers as loops, sometimes "point loops": (10 + 2 x 01) / 3 = 4 from
step 10 outwards
There is not only the 10 room dimensions (Time uncounted): 2
times 5.
All outstretched objects, which the String theory generates,
are called "brans" (membranes): 1-brans
are 1-dimensional strings, 2-brans are surfaces, 3-brans is outstretched
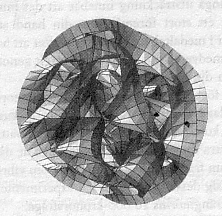
in 3 dimensions etc. If we could believe the illustrations in a TV-program, some open strings are attached in both ends to a surface. Which surface if we only had strings? It must be 2-dimensional membranes (2-brans) - formed by united strings? Compare in our model d-degree 1 with outer poles: 2a ——— 1——— 2b D-degree 1 created by the polarization of d-degree 2, but in our model between complementary poles. (Nothing explicitly or clearly mentioned in the book about such a kind of polarity.) The 6 extra ("undeveloped") room dimensions that the String theory demands and generates have to fulfill form conditions which the so-called 6-dimensional Calabi-Yau-rooms do.
From the book referred to. Original
imprint: Jonathan Cape, London.
We have suggested "radial" versus "circular" structure as first very simple geometrical descriptions of poles 3b---3a. First criticism of this own model included the question how it could be possible to imagine this relation geometrically define surfaces of the 2nd d-degree! Forms as Calabi-Yau-rooms seem much more convincing in this respect. Without knowing anything about the intricate mathematics behind them, we just put a question here if they can be connected with the opposition radial / circular in the purely geometrical sense? Besides such eventual polarities in the structure, we have the
one between structure and holes, a polarity as an underlying =
built-in polarity of next higher d-degree, if interpreted in terms
of our model: "Radial" as connected with diverging Space
(and negative curvature), circular connected with mass (and positive
curvature), an opposition related to Here (again) we could get vague associations to the gastrulation process in embryology: how many dimensions or so-called "independent" directions of growth do we have there: Fig Coelom Another vague association goes to our suggested interpretation of spin 1/2. About 6 dimensions, "undeveloped": Seemingly without any connection with this complicated form (?), in the external, "developed" world, Einstein mentioned the relation between two 3-dimensional celestial bodies as a 6-dimensional system. Calabi-Yau-rooms or the like are thought to exist in every crossing
point of the space-time web. Thus, they remind of what we have
said about "complex poles" in the original booklet behind
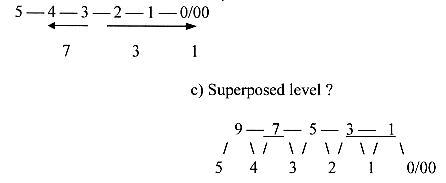
this site: Original poles of 5th d-degree, 0 and 00, may get increasingly more complex character towards superposed levels. That which on one level has the role of a 0-pole, may under its surface, on underlying levels, be constructed by combined 0- and 00-poles, in their turn on a still deeper level being combinations of opposite types etc.
And increasingly more directions will be defined.
There are several such dualities in ST but, as it seems, without any ordering scheme. We have to pick them out from sentences in different contexts and chapters of the book: Structures ----------------- Vibration motions Open strings -------------- Closed strings Bosons ------------------- Fermions, appearing as pairs in the
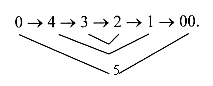
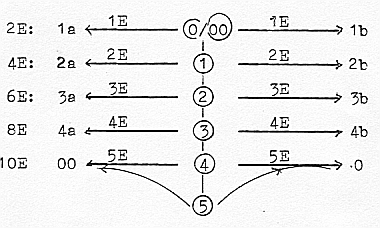
Chain of Motions, d-degrees: 0/00- 1 --- 2 --- 3 --- 4 --- 5
and Structure versus Holes, as corresponding to mass —
vacant space or E = +/- mc2, from polarization of d-degree
4, giving the poles in d-degree 3. This one is of the complementary
type for poles in the same d-degree as we have suggested. So too is the polarity "strings - anti-strings", said to be virtual, occasionally split strings which then join again. We could interpret them as result of the polarization of d-degree 1 → 0/00, from lines to the d-degree of motions, with the "poles" we have called "motions to one another, from one another".
The windings these string - anti-string pairs in ST can form, as loops, seems to illustrate and agree with our naming of those poles.
First the structural oppositions open/closed and "unlinked
- linked" strings: It sounds as if closed strings could be the ST forms of relations between d-degree 1 and one of its "outer poles" 2a or 2b (as inside-outside or similar complementarity), expressed in terms of our model.
Eventually the both types of strings could be seen as just smaller versions of the "radial and circular" poles of d-degree 3 in our model, but they don't seem coupled at all in ST (?). Some open strings were TV-illustrated as bound in both its ends to a surface. No polarity in this surface. Just a bad illustration? But what about the free, unlinked open strings? They seem to be only small, independent pieces of a line? What gives the tension for vibration? Such seemingly independent, freestyle swimming strings in an empty Universe are certainly not in agreement with our model. Looking as something between d-degree 1 and 0/00, the d-degree of motions. In our model nothing is "independent". We can connect this opposition in our interpretation of d-degree
steps, 2 - 1 and 1 - 0/00 respectively, with what is said in the
reference about mass: In ST there is also a more gradual transformation than in our model between structure and motion: linked strings with big radii have big "link energies" and small vibration energies, while those with small radii has small link energies and big vibration energies. What to say about the d-degree
of motions in our model suggested representing
the debranched d-degree in each step towards lower d-degrees,
vibration, rotation and translation?
Perhaps the ST physicists have missed to identify something as
the other "force", the energy of "empty space"
or the like??) We have also the perpendicular aspect on the dimension chain
with lower d-degrees representing 00 in relation to higher as
0, (as geometrically there is an infinity of lines in a surface,
of surfaces in volumes…).
There are traces too of the concept "d-degree steps"
of our model in ST, but we have to dig them out from stray remarks
in the most difficult chapters of the book, from descriptions
and illustrations most difficult to follow and swallow. It's said too that such (or similar?) transitions between forms imply that the number of holes of odd d-degrees in one of the forms are the same as the number of holes of even d-degrees in the other. This too seems to indicate some complicated version of d-degree steps. The author talks about "our conception of drastic typology transitions where the room raptures". In spite of ST being a so much more mathematically intricate and elaborated, scientific version of a model, couldn't we associate these "points where the space-time web raptures" with the d-degree 0/00, the 0- and 00-poles: first points (0), then the 00-pole which we have assumed as the first polarizing force in our model? The 00-pole, which as anticenter and "infinity" represents a non-structure and a phase "before" the space-time "web" is developed or the "non-structure" in the holes of the web? In connections with the M-theory, uniting the 5 different versions
of the earlier theories, these are mentioned with the word "phases".
(Compare starting from 0, from Zero, and starting from the anticenter,
the 00-pole.
There is a lot of talk about furious, violent fluctuations in such things as energies and velocities, even in gravitation, in the microscopic world, within the area of Heisenberg's uncertainty principle and Planck's lengths. The "fluctuations" seem to be only a mathematical conclusion (necessary or not?) from this undetermined or indefinite area of quantum mechanics.
These fluctuations could in our simple model be
interpreted as the motions out of the polarized borderline between
+E and - E or 0 ----00: In some experiments of quantum physics there is a similar relation
between Yes and No answers, particle or no particle, as if the
measurement happened to occur when the fluctuating something was
in the "-E"-area when the answer is no and vice versa.
Three aspects on this: a) The formulations, "smear out", "wrap a surface",
seem to include the concept of superpositions from
quantum mechanics, yet this word is not mentioned. b) Another association to the violent fluctuations concerns our early suggestions that the properties Mass and Charge could be interpretable in some terms of "negative" acceleration and velocity "inwards," that is inwards towards a center, a zero point. As crashing cars get new forms along new coordinate axes in relation to their velocity direction.
c) The "String-coupling constant":
What is indeed the difference between the "string coupling constant" and the relation between an inward gravitational force and outward accelerating force?
Not much is mentioned in the book about the mathematics, and
the whole String theory is still just a mathematical one. It sounds as if we could associate this approach with d-degree 4 and 1 in our model, then step 1 → 0/00.
Newton's gravitation with a big G as inward direction from the
00-pole in d-degree 4, to d-degree 1, the string, Then the elaboration of the theory inwards our dimension chain, towards 2- and 3-dimensional membranes and holes, meeting the 4th dimension as built into the Calabi-Yau-type rooms… From one viewpoint it seems rather natural that they take the
step from d-degree 4 to 1, since one d-degree is debranched in
step (Compare the definition of dimensions in ST as independent "directions of vibrations": "Direction" as our name for d-degree 4, and Motion out of step 1 →0/00. "Vibration" as a 1-dimensional motion structure in d-degree 4.) We have to repeat that the ST-physicists' occupation with Gravitation
reasonably should have touched on the complementary FA-force,
related to Vacant Space, but such a force isn't mentioned. (Compare
G-A and M-E in the figure above, see MEGA-fields.)
The 00-pole and 11-dimensional Supergravitation: In our model the 00-pole of d-degree 4 are meeting the complementary
0-pole in last "d-degree of Motion", 0/00. The
00-pole as an inward directed vector field, identified as
a gravitational force, is redefined through "motions
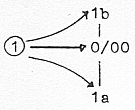
from each other" in the end of the dimension chain. This supergravitation is said to show up if one increases the string coupling constant to a number much bigger than 1 in one of the 5 versions of ST. It's said that no one knows what this "supergravitation" should be! We have described the d-degree 0/00 as the transformation of d-degree 5; also as 5' a starting point for new dimension chains. (Compare poles 1b — 1a, defined in our model as "motions
to and from each other": Or perhaps this theoretical 11-dimensional supergravitation implies
that the ST-physicists, via the degree of Motions, arrive directly
to d-degree 4 with poles of the 5th d-degree, "E-number"
sum 10 (+ Time = 11)?
It seems a bit curious that the appearance of a 2-dimensional
form should be connected with these calculations, leading
to "supergravitation". The condition for this in our
model should be that the calculations were on the way 4 →
3 of d-degree steps, polarization of gravitation and acceleration
outwards (FG and FA),
and a second d-degree debranched in that step, meeting "the
other way around".
Motions "from each other" defines an anticenter, a
(new) 00-pole, a polarization, which should be responsible for
the separation of poles 2a and 2b of d-degree 1, of the "strings",
the tension in these. Upholding them as linear structures. But
the structure of the diverging motions is an inheritance from
the 0-pole of the outward directed vector fields in d-degree 4.
So the question about "super gravitation" could be if it is the divergent 1b-pole, creating a 00-pole, in the d-degree of Motion, that points back to the vector field of pre-material Gravitation in d-degree 4 and its "field lines" ? Back, or forward to Gravitation in a new chain. The R - 1/R duality could perhaps fit into this context. It implies that when the circular size of a linked string shrinks down to 1 (as the Planck length), Universe decreases, but on the other side, shrunk still more, it begins growing again. The ST-physicists gets the same Universe on both sides of 1, an inverse relation. (0/00, the "d-degree of Motion", equivalent to 5 or 5'.)
11) The efforts to unite Gravitation with Quantum mechanics: The difficulty to unite the general relativity theory of gravitation
with quantum mechanics was the cause for the string theory. Operating
with particles as points (0-dimensional) gave "absurd"
infinities of possibilities. These infinities, redefined as anticenters,
are quite natural and necessary in our model. Gravitation is identified
as the vector result of that "infinity", for direction
inwards. There are two statements here worth to note about why
the difficulties arose: 1) Suppose that Gravitation from the 00-pole represents continuum,
the 0-pole the quantified scale in this opposite pair of duality.
Suppose then the graviton, not found yet, is not a quanta
of the same kind as the quanta of later steps in the dimension
chain. 2) About wave functions and squared amplitudes as possibilities
to find a point particle:
As said above there isn't much mentioned about these concepts,
besides that they are defined by different vibration patterns
and the note about mass division between structure and vibration
patterns in linked strings. Charge is connected
with EM-fields in usual physics. A main suggestion in our model
is that this property is a 2-dimensional one, if interpreted in
relation to Mass as a 3-dimensional one. Nothing is said in the
book about Charge, which we could compare with this suggestion,
and it seems that the author sometimes uses the concept of "charge"
in a wider sense.
Strings of ST is thought of as about 10-35 m, that
is hundred million trillions smaller than protons in atom nuclei.
Is it really necessary? Why not blow up the scale?
It's possible, as showed above, to find several similarities
between the String theory and our model here, but only through
searching for them in many disparate contexts and separate sentences
in this reference. The set of concepts used by the theory seems
also to be one of its own to an essential extent. *
|
|||||||||||||||
© Åsa Wohlin:
|
|||||||||||||||
Menu bar:
If your computor doesn't
accept
layers, go here for the links
To the background model
= HOME
Files here
|
2. A 5-dimensional model
- presentation in an earlier version - |
Files
Index to Temperature
in one documen, pdf, 128 pages
Files
Quantum Physics to the end
in one document, pdf, 106 pages
Contact:
u5d
 Calabi-Yau-room
Calabi-Yau-room 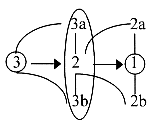 Fig Step 1-2-3
Fig Step 1-2-3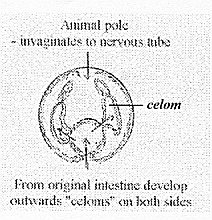
 Fig Complex pole
Fig Complex pole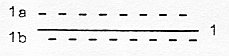 →1a-1b
as virtual strings
→1a-1b
as virtual strings 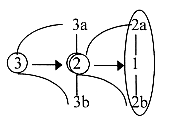 Fig Step 212 marked
Fig Step 212 marked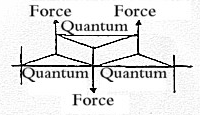
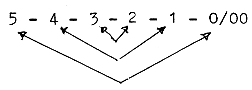
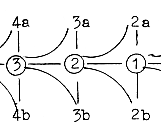
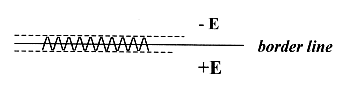
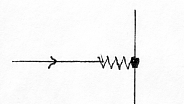

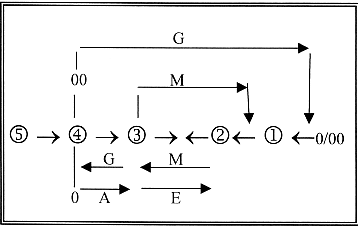
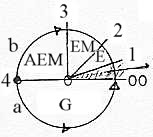
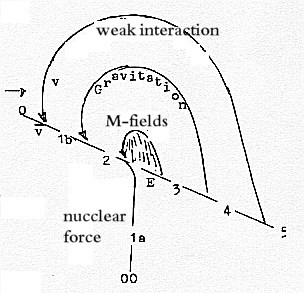
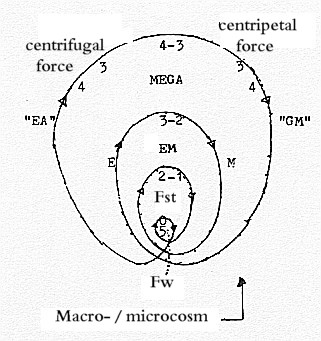
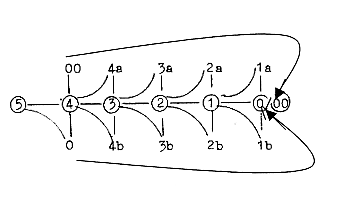 Fig To 0-00
Fig To 0-00