16. "A/Z"-numbers for elements and fusion

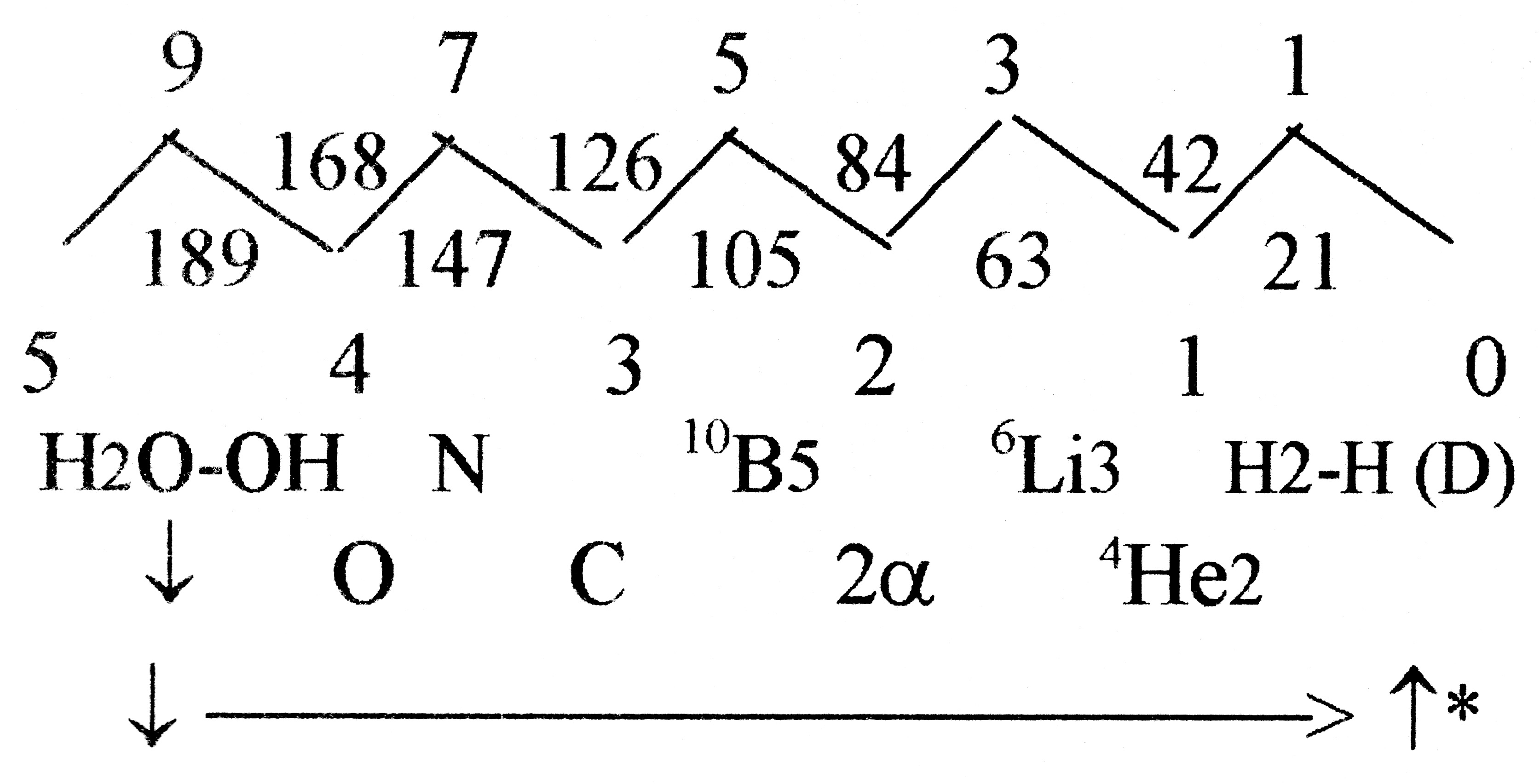
Writing the A- and Z-numbers of elements together as 3-digit numbers, they can be read as sums of 2-digit-numbers from superposed odd chain to the basic series as in figure 10.7:

                  A-Z
C-atoms: 12-6 = 73 + 53
N-atoms: 14-7 = 74 + 73
O-atoms: 16-8 = 94 + 74

Cf. N introduced between C and O, replacing O at chemical synthesis.

Fig.16.1. AZ-numbers of O-N-C-atoms read as sums of 2-digit numbers downwards the basic series from superposed odd series, with lighter elements completing the series

   

*Ionization of water equivalent with a d-degree step 1 —0(00), branched off at the step 5 — 4 . As part of a virtual photosynthesis? (Cf. "NADPH+H".)
   (Isotopes B, boron, 10, and Li, lithium, 6 are both stable but not the most common ones.)

- N + C = 273, the Mv of two ams.

- Fusion could be imagined as illustrated in such a figure: the right part inwards from D to boron (or 2 α as first elementary steps, the left part the carbon-nitrogen cycle in the sun. When O, oxygen, is reached an α-particle get released, which implies a step back to C, carbon again, and the process O ← N ← C is repeated.
   (Life as an outsourced fusion on earth on the molecular level.)

If such a crazy but nice "derivation" of the atom numbers should reveal something, there should be some difference in the inner split (9 -7) and (7 - 5) of the masses of O and C (not an equal or stable division of neutrons and protons), and a split in the Z-number of N (cf. perhaps how N often attracts an extra H as if it had valence 4).

AZ-sums of first 4 numbers from lower 5 to upper 5 = 630, 5 times 126, (AZ of C). Mv of an aa close to 63. 189 + 126 = 315, 168 + 147 = 315, = 6 times 105. After boron 105 the sum is 210..
Sum of 15(27+8) in the x3-series (figure 2.1) = 525 = 5 × 105, the middle number here of boron. 15(27+8), divided 9-6 times sum 35:
    175 140 105 70 35
        315          210

 Exponent 3/2 on lower numbers gives half total aa 1638:
    213/2 423/2 633/2 843/2 =
= 96.23. + 272.19. + 500.05. + 769.87. = sum 1638.34
(These numbers seem connected with the ES-series; ½ x 192, ½ x 544, 500 as 292 + 208, and 770, as 12-group Mx.)

B-chains unbound, counted as AZ-numbers:
N 147 + 2 C à 126 + 2 O à 168 + 4 H(D) à 21 = 819 =
= ½ × 1638.

The ES-series compared with AZ-numbers:
   2 × 147 = 294 = 5' 292 +2
   2 × 126 = 252 = 4' 252
   2 × 105 = 210 = 3' 208 +2…Sum 752 + 4