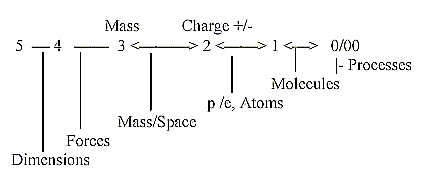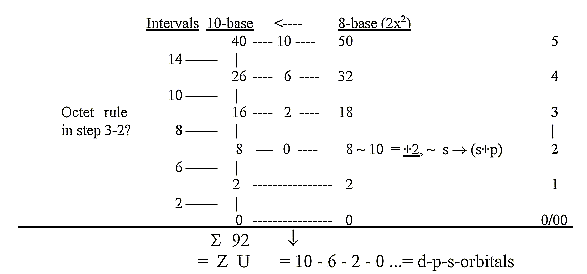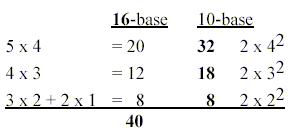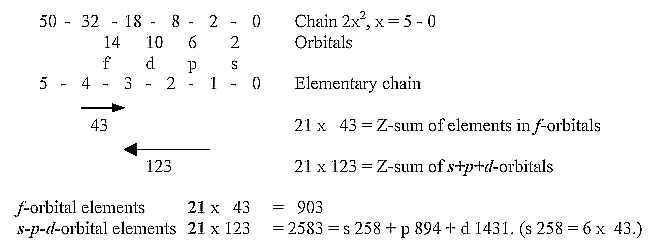In the periodic system as a whole "the octet rule" creates one of the fundamental polarities. (Other ones are the fusion - fission "directions and lightest - heaviest elements. N-Z-relations may be regarded as a third.)
   The octet rule separate more or less oxidation numbers, valences and defines the difference between non-metals and metals. It has been described as a "striving" of the atoms for filled s- and p-shells furthest out and cannot be explained by the elementary balance between numbers of protons in the nucleus and electrons in the shell. Inert gases have this figuration; 2 + 6 electrons, one s-orbital and one filled p-orbital furthest out, which gives a "complete" shell, stability, indisposition to react with other atoms.

From a purely electromagnetic point of view the equal number of protons and electrons itself in every element could have been thought of as making them "self-sufficient". It doesn't. Nor does the structure of orbits according to the reference above. We have to look for some other determining factor.

Why do 8 electrons furthest out represent the most stable configuration, defining whole shells? Here some suggestions.

:

b) 3 polarizations lead to number 8 in the 2x²-chain. 3 polarizations in the2x-chain the same: 1 →2 → 4 → 8, as in d-degrees from 0/00 → 1 → 2 → 3.

c) In our model d-degree 2 has the outer poles (or partial structures) 3a and 3b:
3a—2 —3b: possible to read as 2 + 6.

d) 3 angle steps from 360° - →180°→ 90°→45° implies an 8-division of a circle.
This angle 45° doesn't appear in the orbit structures of s and p above but with the f-orbital (in step 4-3 in the number chain).
   In the loop model we have the connection between step 4 → 3 and 2← 1.
   Loop-model: Step 5→ 4 corresponds to step 1← 0/00 (s) ,
   step 4 → 3 corresponds to step 2← 1 (p).

Fig. 05-2:

Could the completeness of the number 8 eventually be connected with the fact that the coefficient of direction at 45° is 1, sin = cos? A balance between directions "inward /outward, poles of d-degree 4 in our model, as they appear in d-degree 2?

e) 8 space quadrants make up a full, complete Volume (d-degree 3). In the f-orbital only 2 electrons, each with 4 lobes, occupy these solid angles as noticed above. This fact could be thought of as translated into the s+p-orbitals in the lower degrees.

f) Charge as such, as one of the elementary properties of matter, has in this model been assumed as a 2-dimensional one in relation to mass when analyzed as 3-dimensional.
If so, could this imply that d-degree 2, giving number 8 in the 2x²-chain, constitutes a certain border; electron shells as expression for total positive / negative charge?
Mass Charge +/-

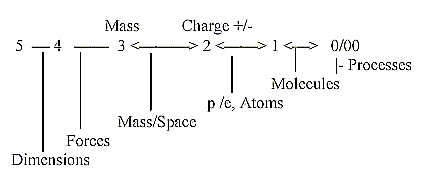
g) A related aspect refers to views on development in this model: from Forces to Mass to Matter of opposite Charge etc. The electromagnetic force assumed to develop in d-degree step 3 - 2 with elementary particles of "matter" as p and e appearing in d-degree 2. In following step 2 - 1 we could assume the differentiation of chemical elements. in next step molecules.

h) Charge as property has naturally roots in higher degrees as d-degree 4. The elementary polarization of d-degree 4 may be written: 4 → 3+1. These figures doubled give 6 + 2, the numbers for p + s-orbitals.

With these a bit different aspects we reach number 8 In several ways towards the middle of the chain (3 or 2) from higher or lower d-degrees, the kind of centre where directions outwards and inwards meet in the loop model.
   Oxidation numbers and ionizations depend more or less on this "octet rule".

Worth noting is that e.g. Cl (17 Z) as a ion Cl- , with 6 e- furthest out, that is with "completed" s + p-orbitals, has a bigger radius than Ar 18 Z. Hence, the "stolen" electron doesn't supplement the p-orbital into symmetry, nor to inactivity. The number 8 itself doesn't explain the inertia of the inert gases. Elements, which through ionization get the full s+p-number 8 furthest out, as Cl-, K+, Mg2+ etc. etc. are actively involved in molecular processes, those gases not.
   Only where this number 8 or filled s+p-orbitals in outer shell coincides with the equivalence between number of protons in nucleus and electrons in the shell, the inertia appears. The geometry of filled p-orbitals may be one factor.

Generally speaking, we should count on dimension chains developed on many different levels and with different relations in the steps, expressed as operators of different kinds working in the d-degree steps. Then the octet rule could perhaps express such a conjunction between two (or more) levels or properties. One example:
   In the dimension chain as Force times Distance (an 1-dimensional potential) the products led to the same number 8 of s + p:

   5 x 4 = 20, 4 x 3 = 12, the lower steps 3 x 2 = 6, 2 x 1 = 2.

On a deeper level, in a dimension chain of forces, the strong force (Fst) has been assumed developed in d-degree step 2-1. With the electromagnetic force regarded as developed in step 3 - 2 and Charge as property in d-degree 2, the first polarization of charge in protons and electrons becomes a condition for the development of the strong force. Cf. the outer poles of d-degree 2 = 3 + 3 = 6: 3a — 2 — 3b . We could perhaps imagine that such processes on different levels coincide at d-degree 2, defining the octet rule?

Could there exist some connection too between the octet rule and the fact that the strong force in nuclei isn't fully developed before » 8 protons?

Transformations of numbers between number-base systems (nb-x):
As said above: the possibility of a connection between different d-degrees and different number-base systems (built on E-numbers as sum of poles) has been developed in the files about the genetic code, the possibility of an inherent mathematical operator on an underlying level to physics and biochemistry (?).

The 2x²-series behind electron shells read as 8-base-numbers:

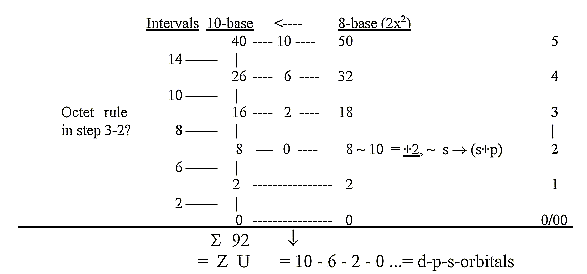
Intervals in the 10-base number chain:
= f-orbital 14, d-orbital 10, s+p-orbital 8, p-orbital 6 (+ s-orbital 2).

Cf. the chain of multiplications Force times Distance and transformations nb-10 to
nb-16:

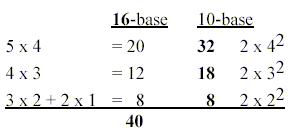
6. Factor 21 and Z-sums divided on elements in different orbitals:

Bi, 83 Z, is often regarded as the highest "stable" element. The whole sum of 1 - 83 Z =
= 3486 Z.
This sum is divided on the elements in different orbitals like this:

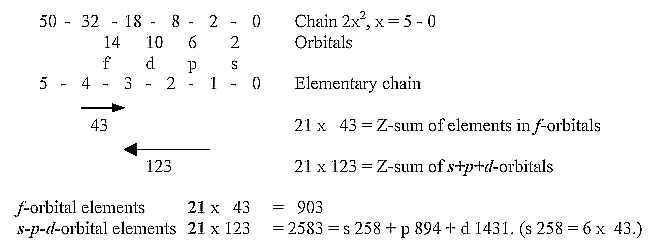
f-orbital elements             21 x   43 = 903
s-p-d-orbital elements      21 x 123 = 2583 = s 258 + p 894 + d 1431. (s 258 = 6 x 43.)

Note the factor 21 [factors 7 (4+3) and 3 (2 +1)].

*

To
7. Metals - non Metals