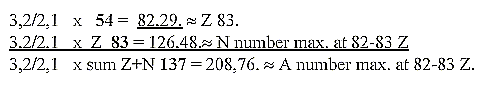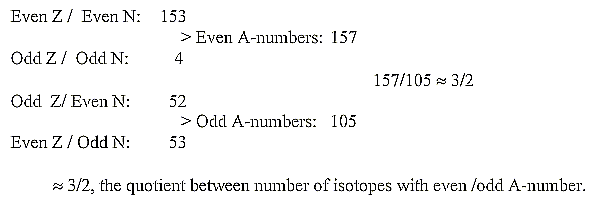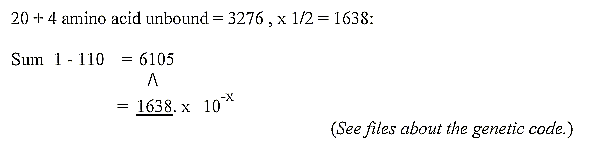|
10. Neutrons and protons - a polarization:
a. Neutrons outside atoms "disintegrate" into protons
and electrons and neutrino radiation. We have in this fact a polarization
step from a neutral mass particle into charges +/-.
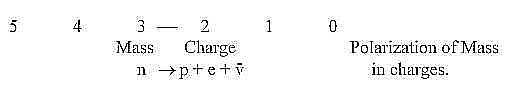
Neutrons seem to have analogous function in multi-proton nuclei
as neutrinos in individual particles, sewing together the structure.
As expressions for a binding force they could
be associated to the higher d-degree in relation to a lower one
according to general views or postulates in our model; where Mass
and Charge as properties have been assumed defined in d-degrees
3 and 2 respectively. The postulates imply that Mass is a binding
force in Charge as said above.
(It's said that according to some calculations
the gravitational force (FG) related to
Mass at first, after Big Bang, was equal in strength with the
electromagnetic force (FEM) related to
Charge - when counting with the whole Mass = 1. Perhaps comparable
with the approximately equal number of protons and neutrons in
the lightest elements (H excluded.)
In terms of the assumed quarks in the standard model, the polarization
of neutrons means the up-quark becoming a down-quark, down-quarks
becoming up-quarks in the proton, i. e. implying a total inversion
of quark "directions" (dud →
udu).
This reversal could possibly be connected with
the opposite directions in our loop model of the dimension chain,
in thirds of charge units: (-1, +2, -1) →
(+2,-1,+2).
Mass — Charge-relation (A—Z)
for elements 1-20 Z ≈432
— 210.
(Triplet numbers from the dimension chain. N = 222 )
b. The quotient n/p increases towards heavier elements in the periodic
system, from 0 →1 (H →
He) to about 1,587 (~ 22/3). in Uranium 238.
One aspect is the fact that smaller volumes have
bigger surfaces in relation to the volume than bigger volumes. This
means relatively more contact with the outer polarizing space (as
00-pole), hence polarizations of neutrons: n →
p + e...
One suggested aspect here is to look at the relation N-Z as in
some sense perpendicular, e.g. neutrons as intervals in relation
to protons as borders: |—| p -
n - p.
They appear as matrices to (or pattern of relations
between) the proton groups. Such a relation could be illustrated
by "chess board" squares with crossing points representing
protons, edges neutrons.
Fig. 10-1:
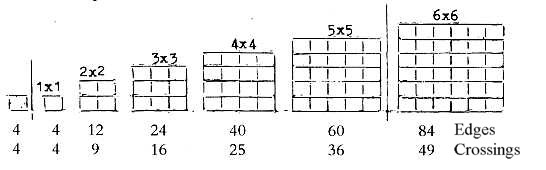
With the extra 1x1 square one get the sum 238 of Uranium
(Why an extra square? What should it represent?)
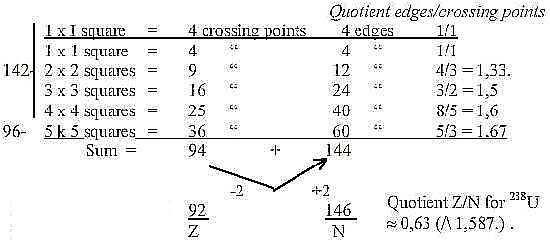
The N/Z-relation of 238U is closest to 8/5, the quotient
at 4 x 4 squares.
When 238U not disintegrates stepwise
through a-emission but is splinted into 2 parts, the partition is
about 2/3: mass maxima about 95 and 140: in Z-numbers: Ba 56 Z (A-number
of isotopes 130-144) and Sr 38 Z (A-number of isotopes 84-95). Cf.
the sum 94 Z above.
c. Development of the N/Z quotient in steps 5/5 →
5/4 → 4/3 →
3/2 → 3,2 / 2:
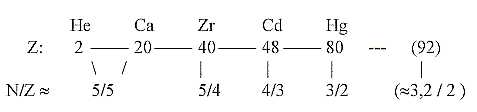
Cf. chain steps of products:
Fig. 10-2:
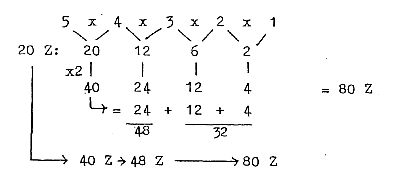 48/32= 3/2
48/32= 3/2
N/Z quotient at 209 - 206 A = 126-124 / 82-83
Z ≈32 / 21:
3 ——
2 ——1
32 21
d. 137 is stated as the quotient between the nuclear force (Fst)
and the electromagnetic force (FEM) in strength
(Gamow). This is the mass number at Z 56 (Ba) in the middle of the
2x2-chain, just after 5 shells in the periodic system.
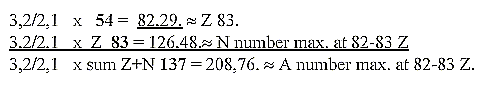
e.. Maximal surplus of N in relation to Z:
U 54 N (238 A)
Bi 43 N (209 A)
f. Even /odd mass isotopes. Number of isotopes and N/Z-divisions:
According to one source there should exist 284 isotopes regarded
as stable ones.
According to a Table on Physics one finds only 262 (of which 41
have unstable isomers).
Division of these 262 isotopes on even and odd numbers:
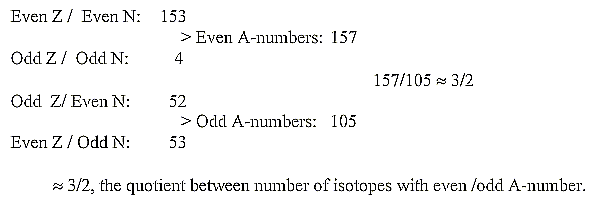
Figuratively the different groups could be illustrated as xn-curves,
n = 4-3-2:
(surplus of N disregarded):

Mean value per isotope for the three bigger groups
≈109,56. . (for all four = 108,01.),
This is numbers around 110, the sum of the 2x2-chain
related Z-distribution in the periodic system. It seems to connect
the 2x2-chain with mass numbers too (?).
About the quotient 3/2 of three bigger
groups:
Compare the total number series 1-238 (A) = 28441 (nearly the same
sum as 28.258 of "stable" isotopes):

g1. Division of Z- and A-sums of 1-83 Z in quotients within a dimension
chain,
elementary or in the 2x2form:
(A-sums more analyzed in Appendix.)

11. Two extra annotations:
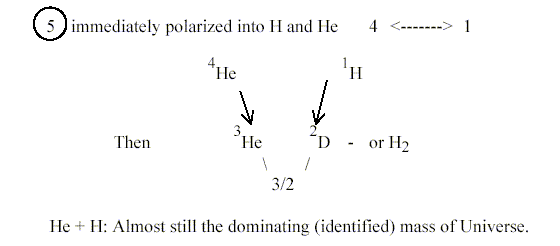
1. A-number 5 and He - H:
Why the mass number 5 doesn't exist at all as an isotope may perhaps
be answered with the suggestion here that 5 is the number for the
whole, the beginning of all.!?
2. An inverse connection between the sum of the 2x2-chain
and sum of 20 + 4
double-coded amino acids in the genetic code:
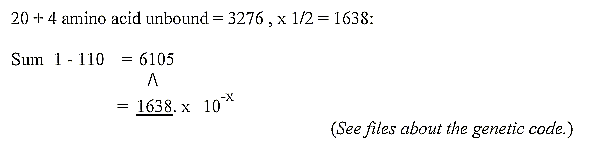
To
Appendix:
More Numbers, pdf
|
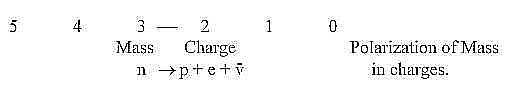



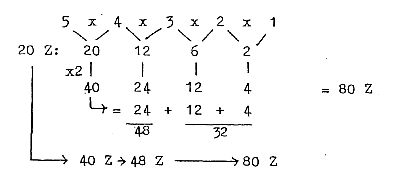 48/32= 3/2
48/32= 3/2