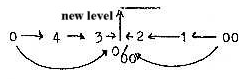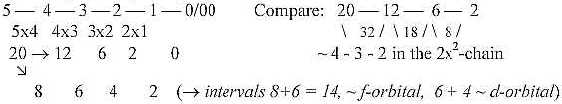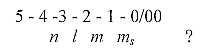|
3. Orbital shapes - dimensional aspects on the
geometries:
Reference here: http://winter.group.shef.ac.uk/orbitron/AOs/5d/index.html.
There are three different aspects on these orbital forms:
- Geometrically the occupied dimension degree of the orbits.
- Form of individual electron orbits as stepwise halved lobes.
- Angle polarization between the orbits of opposite electrons in
electron pairs.
Geometries:
These imply a stepwise increase in occupied dimension degrees (1→2→3)
or orientation in p →d →f-orbits,
as inwards in the dimension chain, in accordance with the increasing
number of electrons.
→ 1: linear: p-orbits along the coordinate
axes
→+ 2: plane quadrants: d-orbitals
also in plane quadrants, 2-dimensional
→+ 3: space quadrants: f-orbitals,
2 of them obviously also occupying space quadrants (solid angles).

The s-orbital illustrates the 0/00-relation between centre (0)
and anticenter (00).
In the s1-orbital one electron in
a pair seems located in the centre or within the nucleus as occupying
0 dimensions. The other one in the pair (He, 2 Z) represents a more
or less undefined anticenter. (This fact could eventually explain
some special characteristics of the alpha-particles and liquid He?).
To fit in the geometrical scheme above we have to regard the elementary
s-orbitals as expression for what in our model is the d-degree of
Motions; 0/00 equivalent with 5' and as such a whole on a secondary
level.
Forms of the orbits:
These imply polarizations as halvings of the form in growing number
of lobes of an electron orbit through s →
p → d →f
-orbits; polarizations inwards in opposition to how lower dimension
degrees are created by polarization of higher ones in our dimension
model when it concerns geometrical structure and where the degree
of motions increases towards lower structural degrees. See annotations
below.
s 1 e = 1 whole sphere, the other "a centre".
Fig 03-1: s-orbital 
p 1 e = 1 lobe. 1 e per half axis: Fig 03-2: p-orbital
6 electrons along the c-ordinate axes.
(An electron pair "dumbbell" formed).
d 1 e = 2 lobes along whole coordinate axes.
3 electrons with halved ("dumbbell"
formed orbits along x-y-z-axes.
1 ring-formed around z-axis in the x-y-plane
(Rotation as a 2-dimenional motion separates x-y-plane
from third z-axis.)
6 electron orbits halved along secondary axes
through the 12 plane quadrants.
f 1 e = 4 lobes. 2 + 6 = 8 out of 14 electron orbits
are halved once again:
One of two possible arrangements is called the
"cubic form":
6 e along coordinate axes, each e-orbit divided
in one lobe, one more "ring"-formed, (similar
as cones* thread into one another with middle in the origin).
6 e in plane quadrants as in d-orbits but here
each e = 4 lobes.
2 e obviously in space quadrants, 1 e = 4 lobes.
* Note that these "conical" forms of the f-orbitals could
be regarded as one partial expression for a 0-00-relation, "outer"
poles of d-degree 4 in our model.
Angles between electron orbits in the pairs:
Regarding the angle or sign relations we also have the polarization
direction inwards, in opposition to our hypothezised order when
it concerns the complementary poles of structure in the dimension
chain: steps 5 →4 →3
→2 implying angle steps 360°→180°→90°→45°.
There is only the same angle relation in the middle step, i. e.
in the d-orbital.
The f-orbital, in number of electrons related
to step 4-3, get the angle relation 45°, in
our model hypothezised as in step 2-1.)

This is descriptions of lowest s-p-d-f-orbitals: the same orbitals
in outer shells get still more divided.
The higher orbitals represent cumulative results,
include the orientations of the lower ones: only 6 of the 10 electrons
in a d-orbital occupy plane quadrants, only 2 of the 14 f-electrons
the space quadrants.
Annotations regarding directions in the dimension chain:
In our elementary dimension chain decreasing d-degree of structure
corresponds to increasing d-degree of motions (d-degree 1 when polarized
into "external motions"). Motions possible to imagine
as more or less substantiated in their patterns:
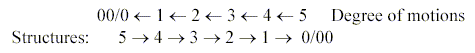
We can remind of the fact that orbits are just patterns
of motions and electrons as "matter"are closest to the
world of Vacant Space as anti-matter on an elementary level in our
model.
We have the counterdirections of the loop model
in these chains but the number of motions is of course much to simple
to apply in this context of electron orbits.
The hypothesis presented in other files that the
2x-chain could be valid from the end of the dimension
chain inwards, is more in agreement with the orbital divisions.
(2 as log-base from the sum of outer poles 1a---1b of d-degree 0/00.
Numbers 5-4-3-2-1 becoming exponents.
To get the 2x-chain in accordance with
halvings of orbital forms above it seems that we have to count on
electron pairs:
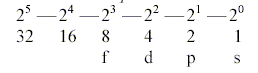
s-orbital, 1 pair: = 1 "sphere", and the
other e as a "centre" counted as 0).
p-orbital, 1 pair = 2 lobes. If all e-orbits were "lobes":
Sum 3 pairs x 2 = 6.
d-orbital, 1 pair = 4 lobes. Sum 5 pairs x 4 = 20.
f-orbital, 1 pair = 8 lobes. Sum 7 pairs x 8 = 56
(Total sum 82-83 "lobes". Cf. total number of "stable"
elements!)
However, counting - more appropriate perhaps - with ring-formed
orbits separately,
the number of forms in first s-p-d-f-orbitals may approximately
be found in an x3-chain
as intervals if rightly counted:
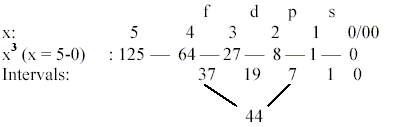
44 = f-orbital lobes: 37 +1 drop- or conical formed lobes
+ 7 - 1 "ring"-formed ones.
19 = d-orbital lobes: 12 + 6 + 1, including 1 ring-formed.
8 = p + s "lobes", counting in that
case with two spherical ones of s-orbitals.
s + p + d = 27 = 33.
Total sum 63, also = 1 + 2 + 4 + 8 + 16 + 32 = sum of 20
— 25.
About halvings of the angle relations, also in opposite direction
to our elementary model: two ways to illustrate what we have called
the loop model;
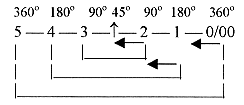 or
or 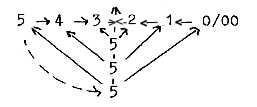
How to account for the f-orbital in such a scheme? It doesn't fit
into the periodic system either, and the aspect here could be one
explanation.
Could we assume that one branch represent a return
inwards, one "upwards" towards a new level (including
new angles)? In that case corresponding to the two forms of f-orbitals,
the "cubic" one and the "general" one in terms
of the reference?
Illustrating polarizations as angle steps in a unity circle, we
get from "2" one branch inwards higher degree "3"
in the figure below, one branch "outwards":
Fig. 03-4: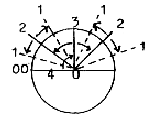 Fig
03-5: Fig
03-5: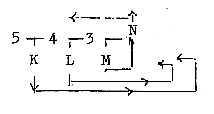
Fig.03-6: 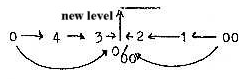
Poles in a 3-dimensional coordinate system (CS):
A simple counting of poles in the CS-system could give an additional
aspect on
the figuration of orbitals:
As poles of d-degree 4 = 0---00 in our model: centre = origin
and (undefined) anti-
centre. = 2 poles .
As poles of d-degree 3 = 4a---4b in our model 8 space quadrants
= 8 poles.
Part of f-orbital: 2 e-orbits = 8 lobes.
As poles of d-degree 2 = 3a --- 3b in our model: 12 plane
quadrants, as pairs = 6.
Part of d-orbital: 6 electron = 12 lobes.
As poles of d-degree 1: 2a---2b in our model: along x- and
y-axes, 2 e-orbits of
opposite signs, together 4 lobes. Another part of the d-orbit.
As pole of d-degree 0/00: 1a---1b in our model: 1 e-orbit
along z-axis with 2 lobes.
+ the ring-formed one - which seems to represent a secondary centre
*. Third
part of the d-orbital. Cf. the division of d-degree 3 in d-degrees
2 + 1.
*Note perhaps also that the ring-formed electron
orbit may represent a factor of uncertainty, that is in the direction
around the z-axes. The "uncertainty principle" possible
to connect with the 00-pole as anticenter in last step.
We could regard a variation of the elementary number chain, assuming
multiplications in d-degree steps corresponding to force times distance:
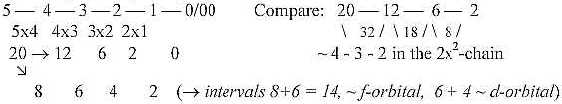
8 space quadrants, 6 outer poles of x- , y-, z-axes. 4 outer poles
of x- y-axes, 2 outer poles of z-axis. In this "energy"
chain orbital numbers appear raised 1 d-degree step.
5 x 4 = 20 = 8 space quadrants + 12 plane quadrants.
First
interval 8 as debranched, disintegrated into 2 + 6, as s + p orbitals.
4 x 3 = 12 = plane quadrants
3 x 2 = 6 = outer poles or half axes in a 3-dimensional
coordinate system
2 x 1 = 2 = poles centre - anticentre, 0 and 00.
Two extra annotations:
a) The thought of a secondary centre in step 3 - 2 could be taken
as illustrated in the orbital forms at spx-hybridizations (and spdx):
resembling a centre - anticenter figuration in the polarization
of signs but here as more separated: half a bigger sphere "surrounding"
a little whole sphere:
Fig. 03-7:
b) The charge curve of the 2s-orbital has been illustrated
like this:
Fig. 03-8c:
R1 /A1 = 4 /1. (Compare figure 03-3 above, polarization
5 →4/1.)
R2 /A 2 = 64/9 = 43 / 32.
Secondary quotient 64/9 ./. 4/1 = (4/3)2.
The quotients could be interpreted dimensionally:
The radius as expression for d-degree 4 defined
by the poles 0 and 00, c and ac.
The amplitude interpreted as expression for d-degree 3, at straight
angle.
Quotient R/A increases from inner to outer maximum
with [4/3]2 - as an expression
for d-degree step 4 → 3. Observe
that this curve concerns the 2s-orbital, not the first one.
4. Quantum numbers n, l, m, ms:
The differentiation of the electron structure of atoms are usually
described through 4 quantum numbers n, l, m, ms:
n = whole shell number,
l = partial shells, representing
the orbitals s, p, d, f above, also describing the
eccentricity of
the orbits in one of the atom models.
ml = the angle
of the orbit in relation to the magnetic axis of the atom, and
ms = spin direction
of the electrons: +/- ½.
The 4 numbers are enough to identify a certain electron orbit.
However, they are attached to an older, more simple atomic model
and they seem not quite easily compatible with the newer views on
orbits described above, especially the l-number.
With 5 whole shells (n) we get 4 developed orbitals (l) = n
- 1, 3 magnetic quantum numbers (ml) = l - 1, divided
in opposite signs: +/- 1, +/-2, +/-3, + 0. And 2 spin directions:
+/- ½.
These numbers of possible states for each quantum
number, 5 →> 4→>3 (and 2) reminds of the dimension model but is it
possible to interpret the different properties which they refer
to in that way?
Here is one suggestion:
- n: The number of the whole shell, expression
for the polarization in inner / outer shells as in poles centre
- anticenter, 0 <—> 00: Concerns also a sphere
in relation to the planes of the l-number. Each whole shell is said
to have a spherical form. D-degree 4 with outer poles 0 and 00.
Or in the latter feature d-degree 3.
D-degree 4-3.
- l: Shape of the orbit planes (s, p, d, f), spherical
to "elliptic". Quotient between the half axes of the
orbit planes describes the transition from spherical to what here
is called a more and more elliptic form. Elliptic orbits imply features
of inward/outward (4a/4b, outer poles of d-degree 3) in motional
direction.
In a secondary sense it could also be regarded
as expressing the opposition circular<—>radial,
in this model assumed as the geometrical poles of d-degree 3, outer
poles in d-degree 2. concerning planes of d-degree 2. ( This
opposition circular - radial could be connected with the orbitals
form along the z-axes in the d-orbital, one electron orbit along
the z-axis, as radial, and the ring-formed one as circular,. and
similar forms in the f-orbital, defining "conical" surfaces?
D-degree 3 - 2.
- ml: Angle of inclination
of the orbit planes in relation to the magnetic axis of the
atom. A polarization along the circumference between planes as an
expression for the step 2→>1
in terms of this older model? Also to be regarded as a crystallization
of 1-dimensional directions around the atom.
(This property seems to correlate with - or express
the same as - the steps between different d-degrees, c/ac →>
linear →> plane quadrants
→> space quadrants in analysis
of orbits in the preceding section 3. In this more elaborated model
the 1st degree is represented by the added or debranched degree
1 in each d-degree step.)
D-degree 2 - 1.
- ms: Spin direction of
the electron pairs, +/- ½: a polarization into
opposite motional moments (or direction of inherent "waves")
as poles out of their connecting lines: an expression for d-degree
step 1 →> 0/00.
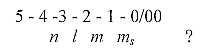
A 5th polarization or quantum number? Probably to identify with
the polarization of an atom in nucleus and electron shell, the primary
centre - anticentre relation?
———————————————————————————
A footnote:
About connections between electron pairs:
Fig. 04-1, 2:
Is two crossing lines - or orbitals possible?
Is it possible for an electron just to change orbit? (Cf. a figure
of Feynman.)
Doesn't such a change claim an underground passage as in the metro?
A way via underlying levels? The further out in an orbit, the more
underlying levels and clutch stations involved.
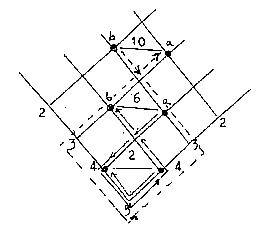
Number of steps demanded for changing
position from a to b = 2, 6, 10 - as electron
numbers in s-, p- , d-orbitals, if the change
demands passing via centre "5":
Fig. 04-3:
*
To
|




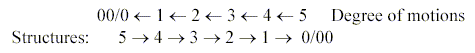
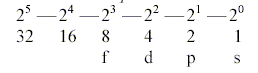
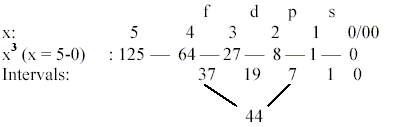
 or
or 
 Fig
03-5:
Fig
03-5: