This file as pdf here.

A little stirring in the conceptual soup:

The model here departed from a very elementary geometrical view on Big Bang as a point (Zero) in the sense of a first center (0). Big Bang as a triple point between metaphysics, mathematics and physical concepts.

The complementary pole (00) becomes really "undefined"- by definition.
The 4th dimension degree (d-degree) as Direction(s) has here been regarded as created between these "poles".

In later years and decades the Big Bang theory has been established as proved, and black holes as consequence of collapsing stars has been intensely discussed.
   Singularities, Zero-points and infinities as 00-poles are incorporated as concepts in physical discussions.
   Yet, it seems that physicists still find it difficult to accept infinities when they appear in their functions. They are regarded as "absurd" answers in their calculations. The String theory was developed as a way to avoid such "absurd" answers when particles were treated as points.

In which sense if any are such answers absurd?
All right, certain kinds of physical calculations may demand that both entities in a relation be well defined within limits.
   However, methods or conceptual structures to interpret infinities when they show up, not neglecting them, seem necessary to develop from the viewpoint of our model.

Two first things to say:
- The redefinition in our model of "infinity" to "anticenter" implies at least that infinities get indirectly defined through their complementary poles, representing centers.
- The 5th dimension degree, here introduced for the Entirety, polarized into poles 0 and 00 makes a difference. The fact that established physics only count on 4 dimensions seems to be an essential part of the problem. The infinities said to appear among the equations in Einstein's general relativity theory may just point towards one such not recognized higher d-degree.

Black holes:

To begin with the singularities connected with theories about "black holes":

"Space-time breaks down" in black holes. This statement or description becomes quite natural if we replace the concept of a "4-dimensional space-time" with the 4-dimensional vector fields in our model, defined through the polarization of the Entirety into the poles 0 and 00. (Of course Space is created through the Big Bang, doesn't exist "before", and the concept "before doesn't exist either.)
   The replacement implies only that a formulation in d-degrees 3-2-1-0/00 (0/00 for Motions, here Time) are raised ( = deepened) one d-degree to 4th d-degree as non polarized At the poles all structure disappears.

In words from Hawking: singularities are found where space-time has a beginning or an end. 0<===4===>000 (4 for space-time). That's obviously at the "outer poles" 0 and 00 of d-degree 4 in our model.

(This picture should be turned upside down.)

In other formulations:
"The singularity is the point where the whole mass of the black hole is gathered and crushed to infinite density".
   "Space-Time breaks down and a so called singularity is created. The density of matter becomes infinite in a place which has no extension".

   Mass→Gravitation → Density:

First, why talk about matter or mass in this context? The problem some authors find in this occurrence seems to depend on their wish to limit themselves within the frame of a 4-dimensional world and the concept of Mass - which in our model isn't identified before d-degree step 4-3.
   That the property of mass as a structure breaks down is quite natural at the poles of d-degree 4. An analysis in terms of a change in dimension degree seems necessary to introduce.

Second, it's said that gravitation seems to grow towards infinity (00) inside black holes. We have identified the vector fields when polarized as F_A, the outward acceleration force (cf. Space, now recognized as expanding) and F_G, Gravitation as the inward acceleration force. With the definition of gravitation as the direction inwards, (Vconv) this growth sounds natural. One aspect on this infinity is the infinite number of directions towards a point. Observe that the infinity here concerns the "strength" of the force.

Third, "density becomes infinite":
Density is in our model suggested as the physical concept in d-degree step 5 - 4. In next step polarized into Mass and Vacant Space (as E = +/- mc²).    (Density as Mass/Volume here implies that a fractional expression may be interpreted as a relation of complementarity.)
   The suggestion is well in agreement with statements about the conditions in black holes. Density of vectors at a Zero point becomes infinite.

Density, it's said too, is inversely proportional to Mass squared:

D ~1/M²

Singularities of opposite kinds, 0 and 00?
The suggestion that Big Bang was a singularity of the 0-type and black holes are singularities of 00-types seems very natural from the viewpoint of the model here. (It is attributed to Weyl [Wikipedia].)
   The 00-pole has here also been interpreted as manyfold in relation to the 0-pole as a unity. Black holes as the death of big stars are naturally a manyfold

In terms of forces:
Singularities are presumed as points "since no known forces can resist the enormous force created when stars collapses".
   The poles 0 and 00 are identified as first binding and polarizing forces in d-degree 4 in our model. Which connections exist between the infinities and singularities in physics and these conceptual definitions?
   In the theories about black holes the anti-gravitational force F_A is regarded as absent. Gravitation, the force of the 00-pole in this model, when acting alone in the collapse of stars, obviously acts as a destructive force since mass disappears. Hence, black holes could be regarded as results of Gravitation in its most primary form. Aggregating but fragmenting or de-structuring.
   It implies that the property of Mass also, not only "Matter", need a factor from the

F_A force for its construction. (Cf. our suggestion to use matter for the atomic structure developed in d-degree step 3--2, mass as concept for the deeper property developed in d-degree step 4→3.)

[At the same time the singularity may be interpreted as a secondary defined Zero-point, as we have assumed a "pole exchange" in the last step of a dimension chain where motions inwards, "towards each other" indirectly defines a 0-pole again. This 0-pole could be attributed the property of a binding force of secondary order (equivalent with what Weyl calls of "00-type"?.
   In that case we have connected the interpretation of black holes with motions, with the last step in the dimension chain instead of aspects in d-degree 4. (Cf. d-degree "0/00" as the meeting of the outer poles in d-degree 4)]

About curvature of space-time:
A factor that may complicate the physicists' analysis is their wish to connect gravitation with curvature of space. Even in d-degree 4.
   In our model a point as the singularity of Big Bang is the opposition to an infinity and gravitation in d-degree 4 is identified as a radial inward directed vector field - and curved space is introduced first in step 4→3.
   In the view of astronomers and cosmologists of today a point represent an infinite curvature, a really self-centered infinity! Such a definition points to the alternative analysis at the end of our dimension chain.
   (Rotating black holes may justify aspects from the lower d-degree. Cf. about rotation.)

As to this curvature:
Would it be possible to replace a gradually increased curvature with repeated steps from an Euclidean to an elliptic geometry? (See file "4-3 III-IV", No. 5)
   An Euclidean plane (as an angle) may be represented by an elliptic line, an Euclidean line by an elliptic point. Applying this description of elliptic geometry in relation to the Euclidean one as a stepwise lowering one d-degree, we may from volumes arrive toward a point in 3 steps.

Space and Time "shifting place":
According to one statement "Space-Time becomes so curved that space and time in some way shift place". It sounds as if we in that case had something remembering of what we have called a "pole exchange" in last step of the dimension chain in our model, where motions from each other define anticenters, motions inwards, towards each other, define centers. (Distance and Time as entities in last step.) In connection with the view on dimension chains of Motions and of Structures as in opposite development, we could perhaps imagine such a change.

D-degree of Motions:    00/0    1      2      3     4         5
D-degree of structure: →5 →4 →3 →2 →1 →0/00

In other words: space becoming the imaginary factor (instead of √ -1 for Time), Time or Motions (d-degree "0/00") realized - perhaps connected with the wild fluctuations of quantum mechanics in microcosm? (Space as "imaginary" could perhaps be thought of as corresponding to human memory, rooms inwards, the world in dreams when a person sleeps and represent "an entirety" in itself.)

What happens at the singularity in black holes - if anything?
Is there any possibility of transformations in the imagined centers of black holes? Any hidden connections with other parts of Universe? The most logical with our model in mind would perhaps be a transformation to the opposite force F_A the outward acceleration force, a hidden connection with expanding Space? With the world of negative energy (E = -mc²)?

Apart from black holes:

Definitions:

Within mathematics the concept poles are used as in our model (also replaced as "partial structures").
   A point Zo is said to be a pole to a function if the limit of the function goes towards 00 when Zo goes towards 0. It's a simple expression for the polarity in d-degree 4 in the dimension chain.

Within physics a singularity is a point in time and/or space where one or several physical entities are undefined "since their value becomes infinite".
   Here the connection between the properties "undefined" and "infinite" is expressed - with the explanation that "we don't know any laws of nature which are valid with infinite values on physical quantities".

A general question: Could some of the problems with singularities and infinities depend on a mix-up of different kinds of infinities and of different aspects or definitions of "singularities"?

One may ask:
What is the essential property of an infinity?
·   That it is immeasurable?
·   Infinite in number of something?
·   Or just unlimited?
·   Or just undefined or badly defined just in this special relation to some other  quality?
·   Or the reference to its relation to a center, a 0-pole, its property as an  "excluded center" in relation to an "enclosed" one? Its character of  "anticenter"?
·    Or the event that some zero point has become inverted?

The several different kinds of infinities and definitions seem unclear or disputable.
   Infinity in numbers is one thing, but there are essential infinities as anticenters that don't concern numbers. Infinities in "strength" of forces, in the property Mass or in Charge are hardly of the same kind; the only common property may be the that they are immeasurable.

Some other examples:
-   3rd degree is undefined for an existence in d-degree 2. We have that higher d-degree is undefined in relation to a lower one, but it could hardly be described as infinite?
-   In simple geometry a lower d-degree represents infinity in relation to or included in the next higher one - as a potential number of surfaces in a volume.
-   A spherical surface is closed and measurable as such but unlimited, in this sense infinite.

We could add a question if singularities may have any connections with the "superpositions" in quantum mechanics?
   A superposition is perhaps not infinite but undefined with respect to 2 possible answers. However, on the x-axis in a coordinate system the y-axis is undefined and could be regarded as representing an "anticenter" and as such all possible but potential values, including +/- infinities. Equivalent with the 3rd d-degree in relation to an existence in the 2nd d-degree.
   If a superposition when released is regarded as a collapsing y-axes, giving answers Yeas or No, it's equivalent with probability 1 or 0. And probability is perhaps the only physical concept that is infinite at a well-defined number 1 (!).

What does a probability on the other side of this border 1 imply? It's said that physicists have met such peculiarities. In connection with Schrödinger's wave functions the probability to find the electron somewhere is the amplitude squared. Then the amplitude must be below 1 (something) in order not to give probabilities >1.
    Could this problematic infinity be self-inflicted? Depending on some wrong border to the possible amplitude? Or on the other side of 1 represent something that already has happened? Backward in Time? )

Does the redefinition of infinity to anticenter imply any contribution ?
It follows from the starting point of Big Bang, all right, but then?
   Infinity leads the thought to size, immeasurable things, while the concept anticenter allows much broader references and points toward a relation.

Transformations:

Everywhere where the 0-pole becomes the denominator, these difficult infinities must show up. There must be something wrong with applying this mathematical convention to physical realities, since the Zero point and Big Bang naturally is a common "denominator" for everything in Universe.
   It seems necessary to analyze what a mathematical fractional number really corresponds to in physical terms. (Cf. fractals.)
   The natural thing would be to see them as relations and indirectly arrive at new definitions.

Again, within mathematics a singularity is an undefined point in a curve, a surface or else analytical function: a point as a break, a corner or such things. It's classified as undefined since some other mathematical concept, whatever it may be, isn't defined in that point.
   A simpleminded view would be to look at these points or corners as polarizing ones, indirectly defined through the continuous or analytical parts that they divide. (Why should every concept which physicists or mathematicians invent have to exist in all other contexts? Not to exist is also a property!)

Such points or singularities of different kinds are related to structural changes as phase changes or to what happens at bifurcations (with reference also to Hirsch and Smile). In terms of our model reasonably with jumps, with dimension degree steps, may it be fractals or whole steps.
   In the latter case it would imply a change, a transformation to another physical quantity. We have the general truth that concepts only can be defined through one another. Hence, it's quite natural if physical concepts will have to be transformed into one another for a definition.

Two possibilities:
Yet, there are two possibilities: with respect to a dimension chain: in the model here:
- Either to find the singularity and infinity of some entity as pointing out a relation to the complementary pole in the same d-degree, or to identify it as expression for a change in d-degree as in a phase shift.

The interpretation may be confused by the general ambiguity regarding the 00-poles in the dimension chain: Each lower d-degree in relation to the higher represents geometrically an infinity. We can also regard a whole chain as "haploid", as a development from the first 0-pole to the 00 at the end of the chain, the 00-pole debranched to a surrounding, an anticenter, in each step of the 0-pole towards lower d-degrees.
   At the same time - or when the dimension chain is regarded as "diploid", all complementary poles in lower d-degrees have inherited some features from the 0-and 00-poles respectively. There is some character of the opposition center - anticenter in each degree (as Mass versus Space, Electric versus Magnetic fields, as protons versus electrons.
   Furthermore, we have assumed as a general view that the anticenter pole, as the "surrounding", is stepwise built-in during the development of the 0-pole towards higher levels. Hence, we can expect infinities built-in everywhere in our ordinary world.
   It's perhaps not strange then that physicists some decades ago found that the positive charge in nuclei seemed to rise towards infinity inwards the center. (Charge in this model regarded as a 2-dimensional property in relation to Mass as 3-dimensional.)
   The found infinity of charge could depend on a mix of d-degrees. It could imply that the analysis should be moved one step deeper to the physical quality Mass, - or outwards put in relation to the physical concept of Distance - in order to get defined values?
   (Cf. the convention to put the negative charge of the electron to 1, and the partial built-in negative charge -1/3 of one quark in the proton in the quark theory. And the family connection assumed here between negative charge and F_A and Vacant Space in higher d-degree.)

Inversions:

A usual, simple illustration of a singularity is the point x = 0 in the function
y = 1/x.

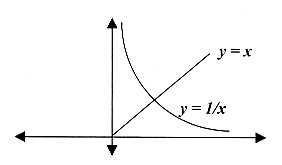
This is the inversion of the function y = x, of a straight line from the origin, a "radius".
   One aspect is the value of y, rising towards infinity when x approaches zero 0. Infinities are of the asymptotic kind. The jump to an interpretation of what these coordinate axes eventually represent in physical concepts seems to be appropriate.
   Another aspect could be expressed as the opposition between "excluded" and "enclosed" center, derived from our first polarization in 0 and 00.
   From the viewpoint of first origin in the coordinate system it's the curve that represents the excluded center, connected with infinities, and the origin (x = 0) with the real "enclosed" center. However, from the viewpoint of the curve, the origin x = 0 becomes an excluded center, and the curve of the inverted function, indirectly defining a new center, represents the enclosed one.    

The functions y = x and y = 1/x illustrates geometrically the complementary poles radial - circular which we have assumed as the polarity from polarization in d-degree 3.
   (See presentation of the model.)

Geometrically it's possible to identify inversions of different kinds.
- The negative and positive halves of the coordinate axes may be regarded as inversions of each other around zero 0.
- Directions inwards and outwards may be regarded as inversions in a similar sense - along the vector lines.
- A part of a curve, inverted along a tangent, would represent the complementarity concave - convex. Equivalent with an inversion of the viewpoint: from outside to inside.

Hence, the complementary poles in our dimension chain may be regarded as inversions - geometrically.
   We could repeat here that one of the poles (or partial structure in all d-degrees has inherited some feature of infinity or anticenter.

Connecting such different inversions with dimensions and dimension degrees, it could imply that also simple inversions of numbers as such around number 1 could content a possible relation between them in a physical context.

Generally it seems necessary to identify "around what" the inversion occurs,
sometimes possible to express as "on the other side of a border".

One could conclude that it should be possible to handle some infinite factors through an analysis of the inverted form and the kind of inverted relation to the complementary pole. If not going underground - to higher d-degrees.

Concerning the physical quantities connected to the poles, in which way if any could these be regarded as inversions of each other: protons and electrons? Mass and Space ? E and M? FG and FA? Surely not in a simple manner.
   A vector field or force as outward directed should certainly have to be turned or "inverted" through the 5th dimension degree, the entire Universe, to become an inward directed one.
   And we can go on assuming that Mass as a property should demand 2 such inversions or reflections, also the one between positive and negative Energy
(E = +/- mc²) to disappear as Mass and reappear as empty Space.
   What physicists call antimatter as antiprotons versus protons demands probably 3 inversions through the higher d-degrees.
    Protons and electrons as antimatter to each other on another level and grandchildren of F_G and F_A surely demand 4 inversions to transform to their complementary pole, the change in mass relation included.

In general words it sounds reasonable that transformations between complementary poles demand reflections as inversions in a different number of steps.

How does this assumption agree with the suggestion in files about Mass and Charge that these properties could be interpreted in some terms of negative (inward) and inverted acceleration (-1/a) and velocity (-1/v) respectively? It may agree in the case of Mass but Charge should need the addition of some more complex operation.

(As to the relation between reflection and inversions, compare about quaternions in file 4-3: V-VI.)

In lower d-degrees where degrees of motions become dominating, "inversions" may be regarded as repeated processes. In light beams we have the continuous transformation of the E-field to M-field to E-field during the propagation. Motion as such, even identifiable in elliptic rotation, implies a repeated "pole exchange", (d-degree 0/00 in our model) as inwards/outwards; so too in longitudinal waves, so in the gait of living individuals.

As to the expression for velocity, Distance/Time (D/T) and last step in our dimension chain, it's possible to regard it as a transformation - or translation - between complementary poles in itself. With the illustration from file Motions:

*

© Åsa Wohlin:
Free to distribute if the source is mentioned.
Texts are mostly extractions from a booklet series, made publicly available in year 2000.