Preceding file I-II: I. Introduction. II. Rotation

III

Geometries

1. A perpendicular geometry:
It is a fact that a perpendicular geometry appears in several physical relations:
   It's pointed out that the gravitational (centripetal) force acts strongest along the rotation axis, while the centrifugal force as its opposite acts along the equatorial plane.
   Other examples: In old physics the orbitals of planets are illustrated as the combination of two vectors, one pointing inwards towards center, one the tangent to this. And we have the orthogonal relation between electric and magnetic components in an EM-wave, as between the amplitude and radial jumps in electron shells.

Most elementary: equality should reign around a first center. Equal distances form a circle, perpendicular to the radius. If divided, it seems natural to think it should be divided in equal parts. Halvings seems to be (or has been given ?) the principle for spin. Quarters for something else - as from a second polarization.
   Hence, starting with a center as first prerequisite, we could see the perpendicular geometry, assumed in d-degree 3, as an inherent, inevitable development from a principally anti-parallel one?

Another aspect: According to our model we have one d-degree of motion in a 4-dimensional vector field, a 1-dimensional, i.e. linear motion, ("to and from each other"), which means a longitudinal one, as variations in density, defining spherical layers in the geometry. The motion moment acts as a polarizing force. (Note that we have proposed Density to be the first "physical quantity" in step 5 → 4, when identifying the usual physical concepts in the dimension chain.) So from a 4-dimensional, anti-parallel structure plus a 1-dimensional motion we get a 3-dimensional geometry defined.

2. Non-Euclidean geometry:
The views above seem much too simpleminded and bound to an Euclidean geometry to explain geometrical realities? What if we look at cosmos in terms of non- Euclidean geometries?
   Scientists say that big masses curve the space around them, but do they tell us why? Masses have positive radius of curvature, the space around big masses have negative curvature. But as far out as one have been able to measure the cosmic space in itself, (the angular sum of a triangle), it seems to have an Euclidean geometry.

Departing from our model we could rather presume that curvatures in the geometries precede the creation of masses or at least are an intrinsic part in that creation and in a polarization Mass - Vacant Space (or E= +/- mc²).
   The surface of a globe has an elliptic geometry; the angular sum of a triangle is more than 180°. The area between three adjacent circles has a negative curvature; the angular sum of the triangle is less than 180°.

An hyperbolic geometry, a combination of positive and negative curvature, is of course the most consistent with the model here, characterized by polarizations. It's often compared to a horse saddle when it concerns surfaces. With this metaphor, there are simultaneously 2 polarizations in the geometry: a step to a perpendicular relation between coordinate axes and a curving of these in negative / positive directions.
   Such opposite curvatures may in fact be identified as transformations of Direction inwards - outwards: the positive one defining an enclosed center, a transformed inward direction, in d-degree 3 a globe as volumes for masses. Whereas the negative one describes an excluded center, as a transformation of outward direction - defining an anticenter as Vacant Space in d-degree 3.


3. Constant positive or negative curvature:
A constant positive curvature, along both coordinate axes of a surface, gives the globular, elliptic form of volumes for masses in cosmos. The hyperbolic geometry rather describes the relation between two such globes with intermediate space: perhaps a reason to interpret what is called "gravitational" centers as responsible for both the attraction and separation between celestial bodies? A manifestation of d-degree 3 of the unpolarized kind of dimension degrees that we haven't been able to find in physical terms?
   Where could we find negative curvature along both axes? Such a form has been compared with two counter-directed trumpets, what is called a "pseudo-sphere". (Introducing a distance between their border circles and positive curvature joining them, we should get a form similar to a spiral galaxy.) The double-trumpet could be described as if each arc of a quadrant in a circle was inverted.
   One example of this geometry could be the magnetic field between 2 magnetic N-poles, forced to meet, repelling each other.


4. Why curvature?
The geometrical aspects depart from 1-dimensional lines. That's a view from lower d-degrees towards higher, inwards in our dimension chain.
   A curved line implies an "intrusion" of d-degree 1 into a 2-dimensional world or a start of defining such a world, a beginning of an orbit plane (a step 2 <— 1). A curved surface implies an intrusion into a 3-dimensional world.
   With the assumptions in our model of debranched degrees meeting "the other way around", Step 4 →3 corresponds to the step 2 <—1.
   The "intrusions" inwards in the chain along the main axis could in very general words be regarded as transforming the geometry between the principally anti-parallel vectors in d-degree 4 into a 3-dimensional geometry with polarized volumes through curved surfaces.
   It seems easier to interpret the curving as built-in motional structures from the end of a dimension chain, with the chain as double-directed, giving us an observable world with 3- and 2-dimensional forms.


5. Centers in the geometry as shrunk or increased:
Another aspect on the non-Euclidean geometries with positive and negative curvatures departs from the description that a surface which grows faster than proportional to the radius squared give a negative curvature, a surface growing slower than proportional to the squared radius gets the positive curvature.
   Now, taking a piece of cloth and pursing it up in the middle (representing a shrinking center or origin), one gets a wavy surface outwards on the cloth as representing a form with negative curvature.
   If adding a piece of cloth into a hole in the center, increasing it, the surface will curve in a positive manner, more adjustable to the football principle.
   Hence, the curvature is depending on the size of the center - or the unity with the role of a center pole (the 0-pole) in our model.
   The negative curvature could derive from an underlying level, a smaller origin or 0-pole from which we have the outward Direction in d-degree 4. With growing complexity of the realities after Big Bang the center will grow more complex and may be thought of as increasing in size.
   The positive curvature and gravitational formation of Direction inwards would follow purely out of this increased center! That is, if we start from an Euclidean geometry.
   The relation between Vacant Space as divergent and Mass volumes as convergent would then simply be interpreted as a relation between center and anticenter, as suggested in our model - with the addition of a Time factor.

A main concept used in the background texts here is "center displacement". Neglecting the assumption of a gradual growth, a center displacement implies that the circumference (as a 00-pole) on one stage becomes the center for the next stage.

In a description of the elliptic geometry it's stated that
a) a line in Euclidean geometry may be represented by a point in elliptic geometry,
b) a plane in Euclidean geometry may be represented by a line in the elliptic one,
c) a solid angle between planes in Euclidean geometry may be represented by plane angle (as 2-dimensional) in elliptic geometry.
   This points towards the interpretation of the elliptic curvatures as of a lower d-degree. The opposite should apply to a the complementary geometry with negative curvature, lines representing (or growing to) surfaces etc. - and points representing lines...
   Such descriptions indicate that we should see the elliptic geometry and the geometry of negative curvature as of different d-degrees. (Or potentially pointing towards lower and higher d-degrees respectively?) Elementary, as there exist an infinity of surfaces in a volume, a higher d-degree represents unity in relation to a lower as a multitude. We have the unity of Vacant Space and the multitude of celestial bodies.


6. A Time factor again - and the curvature of sine waves:
With (another) Time (or "phase") displacement, we have the form of usual sine curves - as projected outwards from a vector rotation in a unity circle.
   The curvature is positive to 180°, then becomes negative in relation to the first part of the curve, a relation between a and b around the inflection point. Curve b represents the concept of an "excluded center". It could be regarded as the curve a mirrored two times in two axes, both horizontally and vertically.

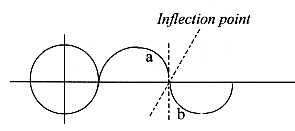
It's the form of surface waves, positive and negative curvature in a mutual relation, as a circle of rotation broken up and polarized in time: We have the opposites convex/concave (representing opposite signs), suggested as one description of the complementary poles of d-degree 2, but following one successively in time.

The inflection points in a 2-dimensional wave make up or define a 1-dimensional line. This is perhaps one answer to the question how on earth the polarization of a 2-dimensional surface in "inside/outside", "convex/concave" may define an 1-dimensional line according to our model !?


Two notes:

a) Hyperbolic geometry in the atom?
In an atom mass volumes with positive curvature is concentrated in the center. Could we eventually find some expression for a negative curvature, if connected with empty space, at the electrons?
   Could an hyperbolic or negative curvature described as excluding a center, be connected with Pauli's "exclusion principle" between electron pairs - or something else in the electron shells? In our views on protons versus electrons we have seen them as "grandchildren" of the opposite vector fields in d-degree 4, children of Mass and Vacant Space respectively (see file Forces).
   Besides this question: In the tentative interpretation of quarks in nuclei as p and n, we have suggested a parallel to the gastrulation process in embryos, including both elliptic and negative curvature in the motional structure of growth.

b) Olber's paradox:
It has been stated that if the Universe eventually had a hyperbolic geometry, then we should be able to find more and more galaxies the further out in cosmos the telescopes reach. However, with the assumptions in our model this conclusion must be wrong?
   If at a certain stage a hyperbolic geometry is polarized in positive curvature of mass volumes and negative curvature of "Vacant Space", then it's only empty space that give the widening lines of sight, and proportionally fewer and fewer galaxies would be found further out. One possible explanation to Olber's paradox?

*

The manifold of masses but apparently unity of "vacant space" should in one sense follow from pure geometries and relations between d-degrees as said above. But how explain the fragmentation of Mass or the multitude of centers for gravitational concentration?
   And how explain the distribution of masses from what is supposed to be a uniform development of geometries from a Big Bang center?
   It has been said that the observed, nearly homogeneous micro wave background radiation in cosmos - taken as supporting the Big Bang theory - has not been able to unite with the "unequal" distribution of masses. It's unclear in which sense it is regarded as unequal.

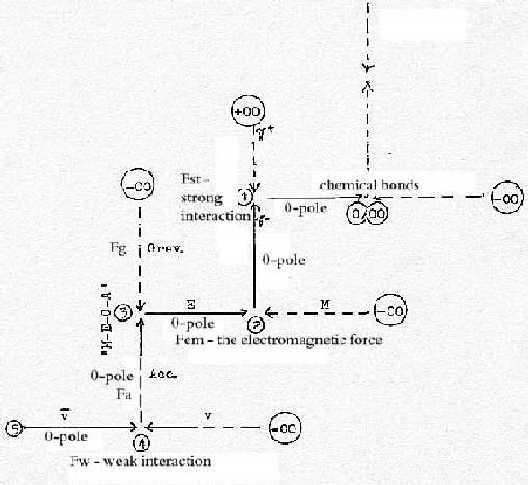
1. Gravitation as a polarizing force!
Gravitation, FG, as an inward directed force with its foundation in the 00-pole is also, according to first postulates or hypotheses in our model a polarizing, splitting force. How can this apparently wrong hypothesis be justified and maintained?

In fact, there is such a polarizing force acting in cosmos, according to the scientists' observations:
   Contraction through gravitation in cosmic clouds lead to a fragmentation, a splitting up of the clouds in smaller clouds and the birth of a great number of stars in groups or crowds.
   It's stated that a cloud under certain conditions (of total mass, density and temperature) begins to contract, and then gets fragmented "in several steps" to smaller and smaller "clumps".
   Secondly, one has also observed a "spontaneous" polarization between hotter and colder regions in celestial clouds, which seems to contradict usual thermodynamic laws.
   The contraction means too that the H2-molecules are split into H-atoms (probably explainable simply through increased temperature?).

Hence, we seem to have first a polarizing force, which could be attributed to the 00-pole of d-degree 4 in our model, then or apparently simultaneous a contracting force, as Direction inwards (pole 4a) in d-degree 3 in our model. A third appearance of the gravitational force in d-degree 3→ to 3b (one pole in d-degree 2) should give the birth of stars and rotation, probably also with a factor of polarization. (Rotation may be interpreted as a "haploid" motion, pointing to another half with opposite rotational direction.)
   Should we talk about Gravitation in all three d-degrees or perhaps give the first polarizing force (00) another name?

2. The polarization principle not recognized as such?
The fragmentation of these celestial clouds is not explained in the sources used here. There is only talk about "small disturbances". The problem seems to be the same as with turbulence.
   A general polarization principle - in several steps, of several kinds or properties and not called attention to as such, partly unknown or unexplained, could be the answer.
   From the viewpoint of polarizing motions (the end of the 5-dimensional chain in our model) and the assumed 1-dimensional longitudinal waves attributed to vector fields in d-degree 4, they should create rings or shells of denser regions.
   It's difficult to avoid the assumption that a secondary polarization through motion of a transversal kind is needed too in explaining the distribution of mass centers in cosmos; some kind of inherent waves in step 2 1 as results of d-degree step 4 →3 in the structure, along the circumferences (compare our hypothesis about side waves).
   Such waves are never mentioned in the used sources. However, the sun for instance is said to be divided in sectors, with opposite directions or signs for the magnetic field - and cells of convection streams.
   Examples, where a general polarization principle intuitively is applied: Pauli's "invention" of the "exclusion principle" between electron pairs in the atom, given the explanation of opposite "spins". The still chiefly theoretical "up" and "down" quarks.


3. Why this "unequal", " not homogeneous" distribution of mass in Macrocosm?
   Scientists mean that the nearly homogeneous background microwave radiation found in cosmos should imply an equally even distribution of Mass in cosmos. This contradicts the irregular or not "homogeneous" distribution of Mass, as they see it. There is no good explanation found.
   In one source used here it's proposed that a rapid increase in size from Big Bang led to the result that different parts of Space "lost contact with each other" which should imply that "local fluctuations" in density could be permanent. Such a description doesn't feels satisfactory, at least not with our model here in mind. "Local fluctuations" and "small disturbances" and such references sound without contact with any scientific principles?
   To approach the problem, we could test to look at dimension chains as a genetic code: We could ask:
   How many (crossing-out) principles of differentiation are needed to explain the individualization of mass in cosmos? (Eventually starting with 4 forces, FA, FG, FE, FM, as there are 4 bases A, G, C and U in the genetic code!)
   For instance: a) gradients of densities, b) gradients of forces' strengths, c) gradients of velocities, d) gradients of radii of curvature, and with Time: e) generations of masses. (Cf. Hoyle's "C-fields".) Perhaps it is enough, or do we have to add chance, fluctuations within the borders of uncertainty in microcosm?
   There is of course no answer here. We could just make the supplementary note that gradients may have the character of discontinuous steps, changing the "quality* of energy" when a certain amount of energy or a certain interval is reached?
* (Said to be the view of Sarfatti 1975.)


4. What creates the many centers? Or how are they identified as such?
Before differentiating processes:
   In our simple geometrical terms the starting point of a vector field inwards has a spread out position with the word from quantum mechanics. The same holds for the first indefinable target of the outward directed vector field.
   Somewhere in the literature it's stated that convergent vector fields (vconv) give an undefined center, as if not pointing to a common, singular one. Why? No explanation in that text. Because the divergent vector field from the primary center already has given birth to a multiplicity of secondary centers, a process preceding the convergent vector fields? Because convergent vectors are pointing backwards in Time - ? - referring to a center already on its way? The convergent field meeting the divergent one "halfway"?
   Such a view could be connected with the idea of an eventual inflationary stage of development after Big Bang.

There exists something of a similar relation between "vectors outwards and inwards in the nervous system: In the inward directed parasympathetic nervous system the nerves depart from the peripheral ends of the vertebral column, from head and tail vertebras (at least in human beings), while nerves from the sympathetic system, outward directed towards brain and muscles, start from the middle region of the spine.
   Ganglions as centers (?) for the sympathetic system are situated near the spine, with many connections with one another, while the ganglions for the parasympathetic system are situated far away, distributed and localized as separate to the neighborhood of the individualized intestines. These are organs developed from within, roughly said from the vegetative pole of the first embryo.

Another question: Should we think of vectors outwards as branched? Compare "bifurcations" at certain stages in chaos research.

It could perhaps be appropriate to apply aspects from quantum mechanics on the question about the multitude of centers. Identifying a higher d-degree is undefined in the lower d-degree, the higher one representing a "superposition", this could imply that the outcome when it "collapses" (here through a d-degree step) may show up as yes or no ( ~ mass or vacant space) - and anywhere? Compare what is said about quanta of forces, that they may have any mass whatsoever, that's undefined. It sounds like one possible answer to the not homogeneous distribution too.

Where do we find the first ovum in a developed human body? An idea about divisions (equal to polarizations?) becomes implicit in such a question, if a parallel to Universe. And copying of a code, which as a suggestion here should be represented by dimension chains as the general pattern within the frame of surrounding conditions and actual Time.

After all, the cosmic multitude of centers resembles turbulence, smaller whirls or bubbles born from bigger ones etc. The long (or protracted) distances between celestial mass concentrations seem perhaps to contradict this similarity but may be a chimera. Expansion of Vacant Space creates the distances, with more or less of negative curvature.
   Very simpleminded: Why are gathered masses so small in relation to empty Space between them? One equally simpleminded answer: The "lengths" of vectors pointing outwards are principally unlimited, while the "lengths" of inward directed vectors gets principally limited by definition at their meeting points (ultimately the black holes?):

5. Bubbles:
Looking at macrocosm as 3-dimensional, as from a 3-dimensional point of view, we may perceive the accumulations or "bubbles" of masses, stars and galaxies, as elevations from a more high-dimensional world. As unavoidable irregularities in a "degraded" space.
   Aggregation of masses becomes " intrusions" from a 5-4-dimensional world into this lower degree. (Is that why mountains are regarded as homes for Gods?)

We have mentioned such "intrusions" from the other direction, lower d-degrees as 1-dimensional lines when curved making "intrusions" in d-degree 2, curved surfaces in d-degree 3. Extra-(or inter-)polation gives "curved" 3-dimensional volumes implying intrusions in d-degree 4: What should such "new" curvature of volumes involve? In which form should it appear? Perhaps just that which Einstein said, that big masses curve the space around them! I.e. another aspect on Space: not only a simple, all-penetrating coordinate system x, y, z, applicable in the same way in masses and empty space, but with another, separate more high-dimensional manifestation in these "bubbles" of masses. (Another possibility is to associate it with negative curvature but inwards, the principle of life!)
   Viewing the development in the other direction: Do the "intrusions" of higher d-degrees into lower ones, of a pole of d-degree 5 and d-degree 4 into d-degree 3, imply something else than intrusions seen in the opposite direction?
   It seems so in one sense: We get the high-dimensional world inside, within the aggregated masses, not as external as with the opposite view.

If a 4-dimensional and partially 5-dimensional reality shall show up and find room in a 3-dimensional world, there unavoidably will be "bubbles" in the x-y-z-space! Bubbles as the result and a solution of he problem.
   Vector fields outwards/inwards have to curl, volumes transform to surfaces, as surfaces into lines, a way of transformations from a hyperbolic geometry with negative curvatures* towards an elliptic one in its adjustment to an Euclidean surrounding. D-degree 0 → 4 →3 →(2)
   (Mass is a very effective way to stow energy. A shirt for volumes of chests gets flat as a surface when packed up. Diagonals reduced to points!)

*Is there a possibility that the meeting of 2 negatively curved surfaces
(or volumes?) - which would presuppose several centers or "0-poles" -
may imply formations of enclosed volumes and the start of the "gravitational force" and the elliptic geometry for masses?

Einstein is said to have imagined the property Mass as one dimension added to the 4-dimensional space-time. It sounds curious and doesn't agree with the views in the model here, but it could eventually be understood in the sense above. (Compare the suggested interpretation of formula E = mc² (file...): mass as 3-dimensional and the velocity c squared as representing two steps from d-degree 5 to 3.)

How is such a view compatible with the fundamental assumption in our model that higher d-degrees in masses, when interpreted as 3-dimensional, are transformed into external motions as rotation? Is it only a question about viewpoints? Is there perhaps no rotation as an "absolute" motion when taking the view "from inside" a mass, the rotation only a relative motion seen from outside in a 3-dimensionally interpreted cosmos? Perhaps only a question about the level - or d-degree - of analysis? Or inner 4-dimensional vector fields as binding forces only partly transformed into rotation in d-degree 3?

The two views on "intrusions" could be illustrated by the perpendicular aspect on our dimension chain - and connected with the development of higher levels versus the process of reproduction, two directions which can be regarded as orthogonal in a dimension chain:

Motions built-in as structural elements

When debranched degrees in first steps of a dimension chain meet from the end of the chain (0/00) inwards in step 3--2, a vertical axes through this step can illustrate a development direction towards higher levels as bubbles of celestial bodies - or atoms.

The one way direction of the chain,

5 → 4 → 3 → 2 →1 →0/00 (~5)

can illustrate a reproduction way on the ground level. What is left of these d-degrees 2 →1 →0/00 may be identified with the external environment in which the bodies move and from which they get their nourishment (as H-atoms or He for the galaxies).

Figure illustrating the thought about Level Development:

At first these views may seem incompatible with our descriptions of Mass and Space as poles of d-degree 3, but the a- and b-poles of a d-degree in our model inherit the characteristics of 00- and 0-poles.
   We may also look at a dimension chain as "haploid" between 0 and 00-poles: (not 5---0/00) and assume that only the 0-pole develops towards intrinsic complexity and "bubbles" in the middle step 3-2, defining enclosed centers, while the indefinite 00-pole as anticenter only is defined through this process, only defined as the environment on each stage: the designing of mass bubbles given from "outside", ensuing from lower d-degrees through the condition: a 3-2-dimensional Space.
   With such views it seems possible to unite the aspect of more high-dimensional bubbles of Mass in space with the suggested elementary definitions of Mass and Vacant Space as complementary "poles" of d-degree 3.


6. About Mass as an effective way to store energy:
Compare with transformations between number-base systems.
   Suppose d-degrees are connected with such different systems. A number in base-10, if first divided in parts, most often give a smaller sum when transformed to base-8, than if transformed as a whole. Yet, a development from higher number-base systems toward lower ones implies growing numbers, mirroring the growth of cosmos.
   In the opposite direction, a cosmos of binary digits may be packed up with higher number-base systems until we reach number 1 (as billions of cells in one head) and beyond that.

To From 4th to 3rd dimension degree - problematic issues,V-VI