Quantum mechanics:

Some possible aspects from the viewpoint
of this 5-dimensional model ?

Most recent reference, David Lindley (referred to below as (L): "Where does the weirdness go? : why quantum mechanics is strange, but not as strange as you think", 1996. Swedish version 2002.

Quantum physics, incompatible with classical physics, includes e.g.

• the double nature of quanta as particles and waves,
• the influence of measurements on the results (or "reality"),
• wave functions of squared amplitudes as probabilities which "collapse" to certainty through a measurement,
  
• the principle of the indefinable (Heisenberg), position and velocity (or momentum) not possible to define exactly with the same measurement,
• experimental results that seem to show "immediate effects" between separate quanta (effects faster than light), and
• fundamental polarizations in opposites which do not agree with classical physics (as directions of polarization of photons passing through a magnetic field).

Physicists still seem to have problems, not mathematical but philosophical or rather conceptual (?), with these results.

Annotations:

1) 4th dimension degree:
Perhaps the most central source for physicists' difficulties to interpret the results of their experiments is their fundamental view of the 4-dimensional reality: 3 dimensions for the space, and Time as one (1): 3-2-1-0 in their mathematics.
   With the 5-dimensional model here and the 4th dimension degree identified as "all-directed" and outwards/inwards as the only relation, we have quite another starting point for the interpretation of "uncertainties" or the "indefinable", the dependence of results on the measurements and so on.

2) Direction in a more narrow sense has of course to be identified - sooner defined - in relation to something else, outside the center, the particle or quantum as such. This thing in the environment as anticenter can be the measurement apparatus.
   Direction, in 4th dimension degree (shortening "d-degree") is in this model seen as stepwise crystallized towards one-way direction through dimension steps.

Is it correct to call it an inherent "indeterminism" as L. does, leaving us as he thinks with the possibility of a "free will"? From the viewpoint of a center there is a direction determined as "outwards". The definition is quite enough for me as a center in 4th dimension degree, in an empty environment.
      As soon as you show up in the North, it's you that decides my direction northwards, a closer determination. There is  most of a "free will" in the center: but it doesn't will or want anything (but possibly outwards) until the surroundings  is met and taken into account and defines and structures its content.
 

3) The uncertainty principle:
One thing is that higher d-degrees always represent uncertainties in relation to the lower ones: a volume contains an infinity of surfaces, a surface an infinity of lines. a line an infinity of points: Which one to choose in a d-degree step will certainly depend on the surrounding.

Some examples of this principle is rather hard to understand as difficulties.
   In Stern-Gerlach experiments where electrons pass vertical magnetic field instruments, they come out with spin Up or Down. L. seems to find it a big problem that it, in this same measurement, is impossible then to know if the electrons have spin Right or Left. This second information needs a new horizontal magnetic field measurement.
   We don't know much about a person before we meet her and talk with her and so on, establish some relation. And different situations can lead to different behavior of that person, naturally.
   Another thing: for a particle along a horizontal x-axis the plus-direction could be "up" and the minus direction "down". In its own right as a center, why should the particle bother about our own external reference to a gravitational field?
   More about the uncertainty in point 4 below and 6.

4) Wave-functions and their "collapses":
Schrödinger's wave-functions (from 1926), telling only about probabilities (for example to find an electron at a certain position), collapses into certainty: "yeas" or "no", when a measurement is done.
   When there is a knock on our door, we can be in real uncertainty. When the person enters, the uncertainty may collapse to a "negative" or "positive" reaction or perhaps Zero. Some persons, as Buddhists perhaps, can reach a state of empty minds in solitude, but find their minds collapsing into definite word quanta when addressed by someone else.

On the level of theoretical physics, wave-functions which collapse could be identified with what in this model is thought of as d-degree steps or quantum jumps:
Simply illustrated:

Or take a more concrete situation: If we follow a wall (or are creeping on it as a fly), a wall as a 2-dimensional uncertainty, and follow it horizontally, we suddenly notice it collapses to a corner, a vertical, 1-dimensional something. Of course we don't know anything about the height of the wall then. Still, with our theoretical knowledge about walls in ordinary rooms we conclude that there must be an opposite corner.
   Following the wall vertically we arrive to a new "collapse", a 1-dimensional "border" or corner, in reality facing towards a 3rd dimension degree, a ceiling or a floor.
On a wall everything is uncertain, not defined, as up-down, left-right until we reach the boundary line to a new dimension degree.
   (If this view on wave-functions and collapses would be sustainable, it should imply, according to the model here, that the property "Mass" could be interpreted in terms of "collapses" of vector fields.)

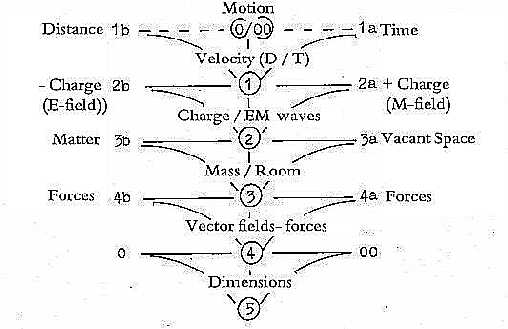
5) Polarizations in opposites:
This principle became a fundamental part of quantum physics through the Stern-Gerlach experiments 1921 (L). They had expected the electrons to leave the magnets in scattered directions, but only got UP or DOWN, RIGHT or LEFT. Classical physics couldn't explain that.
   These polarizations in complementary opposites happen to be the fundamental structuring principle in this 5-dimensional model too, yet not with origin in quantum physics. As soon as we have a center, we have the same principle in the opposites "center - anticenter", "outwards - inwards", with gravitation we have "up and down", we have negative - positive acceleration, opposite charges, kernels - shells, backwards - forwards in relative directions and motions etc.
   In this model, or conceptual structure, different polarization types occur in different d-degrees, which could agree with the view on wave collapses as d-degree steps above.

We could say that polarization is the principle of a "potential", created by in inner "force" in relation to an external "force".

Still, among the first hypotheses in the model here we have presumed that d-degree steps also represent angle steps and give different angles between the complementary poles of the potential. In the experiments referred to the opposition is 180°, presumed to be the angle in 4th d-degree. In relation to direction of the magnetic field however, it seems to be orthogonal or 90°, the presumed angle in 3rd d-degree. (Cf. about E- and M-fields.). And an individual 1-dimensional line in each potential of higher degrees could be thought of as getting the 180° polarity?

In a dimension chain of this model we have the other kind of "polarity" too between directions toward higher d-degrees and direction towards lower ones, outward/inward the chain as such, including more or less of motions versus structure. (Inwards higher d-degrees motions could be thought of as "consumed" and translated into structure as when atoms absorb radiation.)
   We could ask if not some other "dualities" belong to this kind, one of the opposites representing more of motion:
E.g.
- potential - kinetic energy
- amplitude — frequency modulation (as in the nervous system)
- Heisenberg's opposition between position and motion    (velocity, or "momentum"), impossible to define exactly in a classical way in the same measurement, entities that Bohr called complementary, and
- the particle-wave duality.
Also the proton-electron relation could be assigned to this kind, with most of the energy as mass in the proton, most of the kinetic energy in the electron, about equal to the proton in energy if that of motion is included, according to Gamow.)

The two kinds of polarity should of course be related in some way. In the original papers a "haploid" form of the dimension chain is suggested: (as an haploid gamete), which could be written 0 ↔ 4 ↔ 3 ↔ 2 ↔ 1 ↔ 00. Perhaps we will return to it. In any case we don't entirely agree with Bohr's terminology, calling this "duality" or relation between d-degrees "complementary".

6) Superposition:
The physicists talk about wave functions - and phases before they collapse by a measurement in "yes" or "no", "up" or "down" etc., as "superpositions", stages which include both possibilities, not as a mixture of both but in a real sense undecided.
   (According to the 5-dimensional model here they should rather be called "subpositions" with higher d-degrees underlying lower ones.)
   Compare the first criticism of this model (page Presentation of the model): Where to find in the physical world the unpolarized d-degrees 4 - 3 - 2 - 1 ? It seems as if we only can identify the poles 4a - 4b, 3a - 3b etc. Where to find the unpolarized Direction potentially outwards/inwards, where "Volumes" unpolarized into Matter and Space?
   L. says: The true inhabitants in the quantum world are wave functions which per definition are inaccessible for us. We could adopt this statement as an excuse for the difficulty in this model, and as an indication that the underground of our physical reality is pure geometries and mathematics. - as in music.
   Here we assume that a "superposition" corresponds to the underlying next higher d-degree.
   And L asks: What has become of the superposition when the wave function collapses? According to this model the theoretical answer should be: it is to find in the results (both yeas and no) of the collapse in the lower d-degree - plus in a new motion moment. (Compare about Einstein, how a motion of a falling stone can be illustrated in higher, 2-dimensional degree as a "static" curve, a structure.) The simplest example could be a spin 0-particle in the experiments, polarized into +/- spin 1/2, spin here interpreted in terms of motions.

Probably we should allow for real "super"-positions too, lower d-degrees in relation to higher ones, which can implode to the underlying deeper level.

Coordinate axes as each others superpositions:

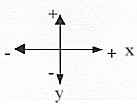
The y-axis is really a super- (or sub-)position, completely undefined, in relation to the x-axis and its direction towards plus or minus. And vice versa. With three dimensions there is a doubled superposition in relation to the two other axes.

(Compare "vertical" versus "horizontal" personalities and their different aspects on who is above and who under, - and their different views on "abstraction levels" as deep down or high up.)

In these experiments of quantum physics we have perhaps the real "inertia systems" which Einstein couldn't find in Macrocosm, born from their own origin and independent of moving, external things?

A superposition which implies that something can be at two places simultaneously is not unthinkable, L says. This should mean that an entity c in the figure below could find itself equally existing in position A and B or virtually translated to these positions. Here this implies disregarding a quantum jump, or neglecting the inherent change of the physicist's viewpoint from one d-degree to another

What causes a quantum jump or collapse of a wave function? For a 3-dimensional unity a 2-dimensional screen for instance? L says there is still a matter of dispute which physical effect brings about that the interference pattern disappears when detection of a photon is made in the "two slit"-experiments.
   A measurement must be "reciprocal ? If something effects the measurement apparatus, some kind of "recoil" must also effect the measured something. Force and counter force. (Newton said it!)
   A photon, a quantum energy of light, is depending on the empty space, on E= - mc², on its propagation, according to interpretations on page "Electromagnetic fields". Hence, how detect a photon without disturbing this intricate interchange and the necessary coherence between the wave packages from two slits?

7) Bell's theorem and Aspect's experiments:
These experiments are said to show more ultimately the difference between classical physics and quantum mechanics.
   There were two instruments instead of only one in each path for photons with spin 0, with the magnetic fields in a certain angle to one another: one way from A to B, the other from C to D. (The angle in the illustration of the book of L orthogonal.)
   The outcome of the measurements at points A-C-B-D could only have the values +1 or - 1.

Bell's theorem: (AxB) + (AxC) + (BxC) - (BxD):
This formula could as a maximum get the value +/-2 if no coupling between different pathways. Aspect's experiment gave the maximum +/- 2 x √ 2:
   Without penetrating the mathematics, could it be wrong to think of a figure like this below?

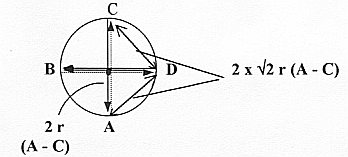
2 r is the distance between A and C, B and D respectively.
1 r, (+ or -) the value at A, B, C, D.
+/- 2 x √ 2 becomes according to quantum physics the maximal value.
   With two measurements in each path we seem to get, or detect, a 2-dimensional system: as a raised d-degree.
   This step seems to confirm the coupling between the 2 dimensions as potentials between outer "poles", as the existence of a short cut, defining the d-degree of surfaces or a 2-dimensional "field".
   We could perhaps presume that each new choice raises the d-degree one step?
   (It is said that the experiment is statistical: only one measurement is possible on each photon. The two angled magnetic fields in each pathway are (therefore?) arranged as a choice, a ramification.)

What if one had three magnetic field instruments in each pathway, angled 3-dimensionally? Could the possible sum of Bell's theorem increase to π or so? The shortest line between opposite measurement points being the orbital as in Einstein's curved space? (Or what if space was assumed to be hyperbolic: should that explain something in the results?)
   

8) "Immediate effects" - and "non-locality":
Physicists within quantum mechanics have big difficulties with explaining the "immediate effect" one particle seems to have on the spin or polarization of the other during such and similar experiments.
   The first to notice is that the physicists' theories and "laws", referred to in descriptions of experiments, always seem to have such "immediate effects": they "know" that the emitted particle has spin zero, or that the value A, B etc. is +/-1, or refer to the "law" that spin always is preserved. We don't doubt it, just notice it.
   Still more immediate effects has the physicists' postulates. So has Einstein's postulate about the velocity of light as the highest possible, That is one severe source to the trouble.

It's hard to understand the logic behind the "EPR"-argument for example. (E for Einstein):
   Two particles move in opposite directions: measuring the momentum (or the spin) of one, gives immediate the value of the other, without measurement, through "derivation". Hence, it is a real property according to E., without any uncertainty or collapsing wave-functions. But it is obvious that "the wave-function" has collapsed in the physical law about preserved momentum or spin, in the brain of E.
   Within the "derivation" through "laws" about preservation hides the polarization principle. With this one accepted, we have accepted too, that one measured particle immediately defines the property of the other - per definition. ("Laws" as "coherence" in the conceptual structure.)
   And different measurements are only different ways to look at the created realities.

Vector fields as another aspect on "immediate effects":
Einstein liked the concept vector fields, rather newly introduced at his time. The concept includes "field lines" as a kind of 1-dimensional entities. If we accept this concept, for "potentials" of gravitation, for electric and magnetic "fields" and others, why not accept that the "field lines" are connecting links, just structures - as a road is connecting two towns. (Cars do not build the road.)

This means that an "immediate effect" can be 1-dimensional - or 2-dimensional etc.
   Why should some "influence" have to "travel" along the link from one particle to the other ? And why should we have to dispute about in which direction the influence was moving, according to L. In which direction goes the road between New York and San Francisco?
   In terms of the 5-dimensional model here motions are derived from polarizations of 1-dimensional "lines". Again: Einstein himself pointed at the fact that we can see the motion of a falling stone in a higher d-degree as a curve, that is in terms of a structure, not motion..
   It seems as if the physicists in some way had cut the Gordian knot and now discuss how the rope's ends hung together.

Concerning velocities:
The conception in the model presented on other pages here is that the "quantum jumps" between d-degrees is so to say "orthogonal" to the d-degree structure or potentials.
   These "jumps" should have nothing to do with the velocities for ordinary objects in classical physics in a certain d-degree. Strictly speaking, why should a d-degree step be restricted by Einstein's postulate about the velocity of light as maximum? Maybe that a motion, born through a d-degree step towards lower d-degree, has such restrictions. That doesn't mean that the step itself follows any such prohibitions.


To be able to brake the restriction of Einstein's postulate, there have been discussions among physicists, who want something to travel, about the possibility of double-directed Time. We can believe in such possibilities without the need for them in this context.
   The relativity theory seems to imply that with two events, A and B, A can occur before B for one observer, B before A for another.
   And mathematically, according to L's statement, light waves going backwards in time are not unthinkable, because Maxwell's equations are 2-dimensional and symmetric.
   Schrödinger's wave function is 1-dimensional with respect to time, and not symmetric, but some physicists have the thought to divide it in two parts, one going backwards, one forwards. (Cf. about force and counterforce above)…. Or alternatively (Cramer) see it as one of a pair of equations traced from a totally relativistic basic equation. (L.)


With Time as an aspect on the relative motions of bodies, it should be possible to see it as partly only potential (virtual) in structures of higher d-degrees, as "built-in" into particles and matter. Rather than talking about "backward" direction of Time we should perhaps in the first place talk about "inwards". (Time is stored inwards in the physicists' minds as memory.)
   Inwards, that is defining a center: perhaps the common source of the two electrons or photons in the experiments could be interpreted as reestablished in this sense. And "outwards" be equivalent with from this center. That would make the concept of "resonance" between the opposite poles reasonable.

About "resonance": it should be possible, according to the model here, to see a particle, interpreted as 3-dimensional, in linear motion as a 4-dimensional system: 3 + 1 = 4: this implying that the underlying higher d-degree of vector fields is activated. It shouldn't be necessary then to believe in some influence "traveling" via the common source to the counterpole of the particle, if the whole system simultaneously exists.

The common source and coherence between the pair of particles is a condition for the quantum effects. And this coherence should imply a kind of "field" in the source.
   Now, a rumor says that empty space has been recognized as representing some kind of energy, at least in Macrocosm.(The"negative" one of Dirac or opposite matter in another sense?). How can we then exclude as L. does every possibility that the quantum pairs has any other correlation than their common source?

L insists that we, in spite of all speculations, need some kind of non-locality, implying an immediate physical effect between the two quanta in the pairs.
   One immediate effect from other contexts is the change of the value of tangent at 90° between plus and minus infinity, and tangens represents the derivative of something, that is a lower d-degree than this something.

Concerning the non-locality, we can simply establish the fact that a surface is one kind of non-locality in relation to a point, and so is a line.

To part 2:
9) The particle - wave duality: