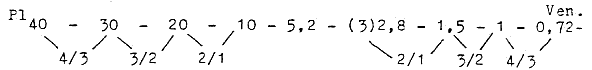Astronomy / - a 5-dimensional model tested on the planet system and other data -
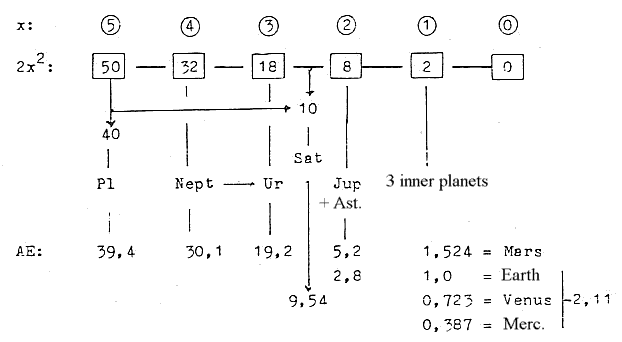
Planet System - Distances in AE
3. Out of a chain 2x2

Sum of distances of the planets, asteroid belt included = ca. 110 AE
    = sum of the chain 2x2, roughly:

This very rough application of the chain on planet distances gives in first steps a surplus which approximates the distance of Mars. ~ 1,63 AE.

Cf. perhaps that in the simple dimension chain behind this (see Physics) one d-degree is branched off in each polarization to lower degrees; in step 5→ 4 we get +1,
50 --> 40 / 10.

The sum 110 gets divided 40 / 70


Some notes:

Saturn's distance 9,54 AE is also = inversion of the square root of the whole AE sum
x 102:
           _______
      1/√109,877 = 9,54. x 10-2.


Saturn in the middle of the chain?
- If we set the inclination of Saturn's orbital plane to zero (0), the sum of the inclinations for orbital planes of all the planets will also be zero, Pluto's not included (Pluto's then 14,7°).
Sums: Merc - Mars = +3,6, Jup - Nept - 3,6 ]


(The asteroid belt between ca. 2,3 AE and 3,3 AE gets the middle value 2,8 AE,
a border between inner small planets and the outer big ones.
110 / 2,8 = 39,3. = circa Pluto's distance.)

Quotients in a more simplified chain:


*

 


© Åsa Wohlin
Free to distribute if the source is mentioned.
Texts are mostly extractions from a booklet series, made publicly available in year 2000

 

1. Planet distances in AE - Exponent 3/2

2. Planet distances
- variation
of Bode's formula - 1/98

3. Planet distances out of a
2x2-chain

4. A graph for planet distances in AE

Masses in Earth units

0. Planet masses
from the Exponent series

1. Masses of planets
from 1/98

2. Masses of planets from
a chain 2x2

3. Masses of planets from
simple triplet chains with exponent 9/4, [3/2]2

*

Latest updated
2022-09-29
*