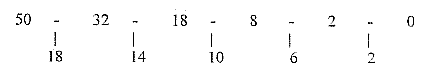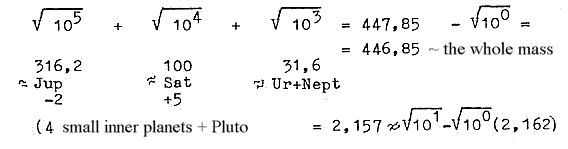Astronomy / - a 5-dimensional model tested on the planet system and other data -
Planet System - B. Masses

2. Number readings in series 2x2    and root of 10-powers 5-4-3 + 0

1. The 2x2-series with x = 5-4-3-2-1-0, behind the periodic system:


Cubic roots out of number readings in the chain::



Saturn ? - As a difference ?

Reading inwards:



Some notes:

   Half the chain, x<2 = 25 - 16 - 9 - 4 - 1:

   [25-16-9-4]1/3= 63,14, + [32-18-8]1/3= 94,9. ~ Saturn


(With interval numbers: [8-6-18-10]1/3= 95,163 ~ Saturn )


Interval 10:

   [10]1/3= 2,1544 = 1,977 + 0,177 = 4 inner small planets + ~ Pluto

Why should mass numbers be derived as cube roots out of a chain giving the sum of distances? Mass assumed as a 3-dimensional property in relation to 1-dimensional potentials or distances (see Physics) ?
   Compare the assumed interpretation of Mass as a property created in inward direction, as "inverted" fields: dimension degree 3 eventually then turned to 1/3, not only a negative direction. A polarization 3 <-------> 1/3 between Vacant Space and Matter.

(Compare the opposite: stars where the radius is inversely proportional to the cube root of the mass
   r ~1 / M1/3.)

2. The root of 10-powers with exponents 5 - 4 - 3 etc:

   √ 105 + [√101 - √10 0 ] = 318,36. ~. Jupiter

   √ 104 - [√101 + √100 ] = 95,84 ~ Saturn

*

 

 


© Åsa Wohlin
Free to distribute if the source is mentioned.
Texts are mostly extractions from a booklet series, made publicly available in year 2000

 

Roots of 10-powers
with exponents
5 - 4 - 3
Down

1. Planet distances in AE - Exponent 3/2

2. Planet distances
- variation
of Bode's formula - 1/98

3. Planet distances out of a
2x2-chain

4. A graph for planet distances in AE

Masses in Earth units

0. Planet masses
from the Exponent series

1. Masses of planets
from 1/98

2. Masses of planets from
a chain 2x2

3. Masses of planets from
simple triplet chains with exponent 9/4, [3/2]2

*

Latest updated
2022-09-29
*