Curvature of Space and some views on motions in macrocosm

The subject curvature has been treated at greater length in files within Physics. 1. The geometry of cosmos is a much discussed question. Is Universe as a whole positively or negatively curved? Interpreters of Einstein's relativity theory have meant that he has replaced gravitation as a force with the concept of curvature of space. Einstein's view on Universe has been compared with the surface of a horse-saddle.
   When it's said that the concept of gravitation as a force my be replaced by the curvature of space, it seems that something like the gravitational force nevertheless slips in through the back door through tensor concepts in Einstein's equations? And apart from that, it remains to explain why space are curved around big masses, why the geometrical properties of space is different around these than in interstellar mediate space between them.

From the viewpoints of our dimension model here it seems reasonable to state that Universe must be both positively and anti-positively* curved, at least in d-degree step 4→3 (and more like a horse than a horse-saddle). *(Product of +R and -R becomes negative, R for radius of curvature.)

The questions about curvature have been connected with the question if Universe is finite in size or infinite.
   Presumably too Universe is neither finite or infinite in a quantitative sense (additional), but both in a qualitative - this with the redefinition of "infinity" as anticenter in the model. Size as a property is created through Big Bang and the further development. It concerns relations - relations between parts of the whole. For Universe, per definition including everything, there is nothing "outside" to compare with, the concept size loses all sense.

To regard cosmic Space as such, as some kind of abstract network with own existence, an entity in itself, becomes nonsense, both in our model and according to a lot of scientists. Its reality lies in relations and is depending on its complementary part, the masses. The polarity is expressed in the formula +/- E=mc2. Here the negative energy E (as Dirac's holes for positrons) has to be interpreted as not just lack of energy but an alternative form, that means as antimatter on a fundamental level.
   Hence, with Space and Mass interpreted as the complementary poles (in d-degree 3 ), the masses with positive curvature get the "matrix" or counterpart in an anti-positive curvature of Space.
   It's also an accepted apprehension of later years that masses as galaxies are carried away by expanding Space (not flying themselves).

Choice between concepts optional?
May we regard interpretations in terms of curvature and in terms of forces as equally
valid? The views and definition of forces in the model here are ultimately geometrical    With the assumptions in the model that a dimension chain also corresponds to a series of angle steps, curved lines are in fact postulated. (Curvature could in that case in reality be quantified.)
   The concepts of curvature seem bound to a view in dimension degree (d-degree) 3, a concept which may lose its sense if we could apply a 4-dimensional aspect?
   Curvature and elliptic versus hyperbolic geometries could be applied to the forces as vector fields as such in lower d-degrees, using formulations in terms of Acceleration outwards (the FA -force) and Gravitation (FG ) as acceleration inwards. (About the forces here.)

In our dimension model one degree of structure gets debranched into external motion in each dimension step 5 → 4 → 3→... And the d-degree of analysis is optional.
   With forces per definition closely related motions a such, this implies that aspects on curvature in macrocosm could concern these motions. For instance the "expanding" of Universe. The apparently high escape velocity of distant galaxies could be the expression in d-degree 3 of a static - and "straight" outward/inward geometry in d-degree 4, when this is transformed to lower degree and Space to anti-positive curvature?
   Corresponding "motions" for masses becomes the 2-dimensional rotation as an elliptic geometrical form.

What should create an anti-positive (-R) curvature of Space?
With the simple illustration of a cloth that is pursed up in the middle, a piece of the radii in the centre shortened, one gets accelerating breadth of the surface as "wave tunnels" outwards. Pursing the circumference instead leads to the football geometry.

With this illustration, the centre as "drawn" underground, should be the first singularity at Big Bang, the first 0-pole, coming to represent an underlying level in relation to the first materialized macrocosm.

Higher d-degrees underground (both 0- and 00-poles in d-degree 4), inside lower ones, as underlying level, should potentially generate a curvature of both -R and +R. "Externalization" of these higher d-degrees as lost in the geometrical structure, as debranched and transformed into external motions - according to fundamental postulates - becomes a condition for both anti-positive expanding Space and positive curvature as mass aggregations.

Centre displacements:
All curved lines or pathways in cosmos could perhaps principally be regarded as following from centre displacements in relation to first primary 0-pole and level developments.
   The hypothesis is then related to escape velocity: The further out from a primary centre a pathway starts, the lower the energy, the more curved becomes the pathways. (Cf. satellites,)

Centre displacements - escape velocity,
cf. steps 5 → 4→ 3:

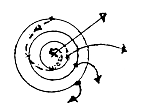
Fragmentation of Mass:
An only positively curved surface defines and includes one centre (1). An anti-positively curved surface defines instead (partly) 2 or more excluded centra. Hence, a Space with anti-positive curvature, should become a factor in the fragmentation of masses in Universe.
   Cf. in last step of our model: "Motions from each other", outwards, with the root in 0-pole of d-degree 4, defines anticentra, while "motions towards each other" with the root in first 00-pole of d-degree 4, defines new 0-poles.
   It's observed too on a real macrocosmic scale in Universe that huge, seemingly empty parts of Space separate huge "highways" or accumulations of galaxies, pointing to the possibility that a more fundamental and elementary geometrical polarization Mass ↔ Space lays behind and before the later fragmentation steps.

Multi-layer creation through anti-positive curvature inwards?
The most characteristic feature of life is anti-positive curvature turned inwards, developing inside positive curvature.
    This combination is illustrated on the biological level in embryonic growth, where surface of the cell grows faster than the square of the radius, resulting in multi-layer creation within first, surrounding "positively curved" layer.

Are there processes in the inorganic world that could be understood in similar terms?
"Disturbances" from outside on big hydrogen clouds in macrocosm or other such concepts which astronomers and physicists use?
   The nuclei of atoms can be analysed as shells - also according to physicists. Could we here eventually have a negative curvature inwards in heavier nuclei in the relation "empty" space / mass, or energy -/+, which makes the nuclei labyrinthianly multi-stratified? Cf. that charge is said to be built up inwards in heavier nuclei.
   The concept "isospin" is perhaps not only a mathematical help concept? Maybe also an expression for the "nutrient supply" of the atom, (its dependence on nourishment as "empty space"? (According to assumptions about light waves in Physics here.) For energy metabolism of the nucleus? In that case there should perhaps exist gateways in the potential wall around nuclei for this import of nourishment!
   Is it possible to imagine that such multi-layer structures in macrocosm - as the rings of dust around planets, planet systems, spiral galaxies, perhaps star clusters in a first phase, could be regarded as a similar patterns of invaginations and openings for the incorporation of matter to "shells" ?

Some added associations:

a) With the anti-positive curvature, implying a kind of potential acceleration of higher degree, regarded as expression for and result of a level underlying masses, it would be possible perhaps to interpret this underlying 4-dimensional geometry as cause to events where these masses throw out surpluses of matter, as cause to star explosions, protuberances etc. That means to interpret such "radial" occurrences in stars (or galaxies?) in geometrical terms of the anti-positive curvature of space. An extrapolation of the ordinary geometrical views on curvature?

b) The negative radius of curvature is usually in d-degree 2 illustrated by triangles with angle sum less than 180°. (Combinations of such triangles may formally enclose positively closed, perhaps elliptic, volumes.) In projection the magnetic field around the earth forms such narrower angles at the poles. They may be seen too as doubled in the field-free area between two magnetic poles of the same kind, two N-poles or two S-poles.
   One perhaps more relevant "metaphor" or expression for this geometry is the fibre directions around germs (or start) of branches in a tree trunk:

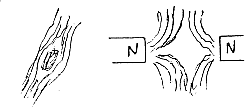
c) The double nature of light:
Could perhaps the double nature of light as waves and particles be interpreted in terms of the concept curvature?
   When a ray of light is sent through a small hole in a screen, it behaves and is detected as a particle on a detector screen if the hole is bigger than the wavelength of the light. But if the hole is smaller than the wavelength the beam may be described as broken up, behaving like a wave.
   In this latter case it seems as the hole got the role of an underlying centre, (as if the beam became "pursed in the middle"). Would it eventually be possible to interpret the wavy pattern of divergence in terms of negative (or anti-positive) curvature?

Olber's paradox and the red shift of light in macrocosm:

The expansion of Universe explains this shift towards the red spectrum in light from more distant stars and galaxies. The same expansion theory is also part of the explanation to "Olber's paradox", the fact that the night sky is mostly dark in spite of the enormous amount of stars in Universe. The answer is said to be that the stars farthest away from us have such a high escape velocity that their light hasn't reach us yet or cannot reach us. (There are other hypothetical explanations too among scientists.)
   The question here is of these same things could be explained purely by the negative radius of curvature in "empty" space and its geometry:
   If Space grows faster than proportional to the cube of radius (and mass the reverse), a beam of light through space have to take longer and longer jumps for its propagation, equivalent with accelerating wavelengths.

Growing steps, growing lambda through the negative curvature of space:

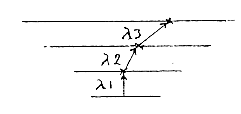
And, if so, much light from distant stars might just pass by our planet in curved pathways, when empty Space grows towards us - from the point of view of the emitting star?

A picture of split light which perhaps passes by our Earth:

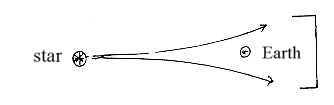
Both theories, the dynamic one about expansion of Universe, and this static one about the negative curvature of space, could be equally valid, only different aspects on the same thing. In our model we prefer to regard the two aspects as a stepwise process in time, where one d-degree of structure (in d-degree 4) gets debranched and transformed into external motion in next lower d-degree.

One scientists' explanation of Olber's paradox builds on the assumption of a fractal distribution of mass in macrocosm (see Wikipedia). This seems to be in agreement with the model here, said without closer knowledge.

Two other annotations:
One author has in his book about astronomy proposed that the light only "gets tired", as an explanation for this displacement towards the red spectrum. Why in that case?
   According to our interpretation of light propagation through cosmos, this propagation is dependant on the negative energy of empty space for its continuous existence. The empty space may not have the same quality everywhere, it may have been exploited by heavy masses for instance and represent different degrees of negative energy. A "tiredness" of light should then depend on the lack of a qualitative nourishment! (About vacant space here.)

Another thought: Universe is criss-crossed by myriads of beams of light, and a plenty of them must have the same wave length and also meet anti-parallelly - perhaps especially so over big distances.
   Why shouldn't they - reasonably - cancel each other out through interference?

Motions in macrocosm:

Rotation:
Most obvious fact in cosmos is that all celestial bodies rotate. A tendency to rotation is also observed in the gigantic H-clouds out of which stars and galaxies are born. It's disputable if the scientists have given any good explanation for this rotation. To quote one such explanation:

"All celestial bodies rotate because of the law of conservation of angular momentum. This is one of the most fundamental laws of the universe and comes from the fact that the laws of the universe do not change dependant on the direction we are looking.
   All celestial bodies have at some time condensed out of large clouds of gas and dust under the influence of gravity. These clouds were probably moderately turbulent so most of the angular momentum cancelled out but there would always be a small residual in one direction representing the net rotation of the whole cloud...."

The explanation doesn't feel very satisfactory: Note that angular momentum is not explained, however conservative it may be, and its origin is just vague suppositions. Remember too that also elementary particles of microcosm rotate, hardly explained in that way?

We could associate the quotation above with the many studies of the problematic turbulence as such and how "radial" inflows get translated to whirls and circular outflows, or how just 2-3-dimensional circular streams and waves appear in liquids.

Could rotation be interpreted in terms of how the centrifugal force (out of FA ) manifests itself in d-degree 3 as answer to - or when combined with - the centripetal force (out of FG)?

Or, in other (?) terms: Could rotation and first angular momentum have its origin in an angle between the magnetic axis of a body and what comes to be the "rotational axes"? An angle decided by inherent d-degree steps between poles, e.g. the forces FA - FG , then FE - FM ? Two coordinate axes, in a smaller angle of decreased d-degree, which in itself give the basis for the concept angular momentum ? (M- and E-fields as polarized from the EM-force born in d-degree step 3-2 in a dimension chain of forces, according to suggestions here. Angle steps hypothetically assumed as halvings: ...180°→ 90°→ 45° →22,5°.    (Generally the steps in our dimension model is hypothetically assumed as also connected with angle steps, in step D4 → D3 180°→ 90°, implying a change from radial to tangential (perpendicular) relation.)

Relations between rotation and other phenomena:

a) There is a formula for the relation between the time it takes for a blast wave to propagate from the inner of a mass to the whole mass and the shortest possible rotation time, called "dynamic time scale":
   It points to a translation or transformation process (or jump) from linear L-waves of d-degree 4 in our model to d-degree 3 and rotation speed. A dimension step.
   It's said about the Crab nebula that the rotation energy of the central pulsar gets "translated to" the whole nebula. (The source does not tell how.) Do we here have a small step towards rotation as a solid body, as friction, revealing the polar combination of radial and circular forces?
   

b) There is also the relation between shortest possible rotation time (Rt) and density:
The time is inversely proportional to the square root of mean density:

Rt ~1 /√density.

I. e.: Higher density implies lower rotation time, = higher rotational speed.
   Density has in our model been assumed as the only and first concept for the "physical quantity" in d-degree step 5 → 4. (As the Mass and Space concepts follow out of next step 4 → 3.). Then we should have two operators in this step, the square root of x and inversion.
   With the loop model of a dimension chain, steps 5 → 4 → 3 → are connected with steps (← 2 ← 1 ← /00 from debranched degrees meeting the other way around, here as motional patterns:

Rotational speed of 3-dimensional bodies:

Inversion as expression for "the other way around"?

c) The rotation velocity has also a relation to the spectral type of stars: hot O- and B-stars rotate about 10 times faster than cooler G-stars, the type of our sun. Why this is so the astronomers don't know, at least they didn't a couple of decades ago. It seems to contradict the formula above, if density of at least the cores in stars are increasing from O- and B-stars towards G-stars for fusion of heavier elements. (Mostly only He-synthesis in O-B-stars.) See file Stars.
   Has perhaps the formula Rt ~ 1/√density above a limited validity? Could it eventually concern the vertical line through middle step in the figure above, with reference to figure 6 and figure 11 in file Stars: decreasing speed of rotation towards the middle step? It's very high for neutron stars (still higher for black holes if they rotate at all?). Corresponding to O-B-stars at the other end of the chain? If so, the problem could support the loop model.

The problem seems connected with that of stars where high surface temperature seems opposed to high temperature and density in the cores.

There is also such examples as these of the relation between density and temperature:

More of structure as bound kinetic energy in colder clouds.

Parenthetically: Could neutrinos and anti-neutrinos be connected with the properties Density and Temperature respectively? In files about forces, the weak interaction force is hypothetically assumed as derived through step 5→ 4 (Fw1) and 1 → 0/00 (Fw2) in the dimension chain of forces. Fw1 and Fw2 connected with neutrinos and anti-neutrinos. Cf. density, neutron stars and p + e- + anti-ν → n.

d) Stars as our sun doesn't rotate as a solid body. The rotation time one turn at the poles is 37 days, at the equator only 25 days. That's a relation about 3/2.
   Could this relation be interpreted as an expression for d-degree 3, represented by the central rotational axes, and d-degree 2 as the equator plane? According to the principle of more kinetic energy in lower d-degrees.

e) Rotation in galaxy clusters seems only partially developed. This observation agrees with the views regarding levels of mass organization in macrocosm, where this highest level gets its character from d-degree 4 or step 4-3. Rotation assumed as the motional pattern developed in d-degree 3, (figure here).

f) When rotation around secondary and tertiary, external centra is added, it may be said to illustrate 3-dimensional pathway motions; a consequence of rotations on different levels of mass organization when it concerns planets around the sun or stars around the galaxy. In these cases it could simply be regarded as a 3-dimensional motion in d-degree 2, since planets are born out of more or less 2-dimensional dust rings around the sun and stars in the "plane" around the galaxy.
   This complex winding up of masses have similarities with the winding up of DNA in several steps to compact chromosomes.

How look at other types of motional patterns than rotation in macrocosm, processes illustrating other d-degrees in compliance with the model here?

Vibration (D1) - pulsation (D4). - Pole exchange (D5), d-degrees of motions:
We have to regard the 4-dimensional vector fields both between masses and within them, as underlying level in matter.
   We have to identify formations of layers (structures of d-degree 2) within masses besides the formation of orbital planes separating masses.
   And where to look for 1-dimensional structures with 4-dimensional motions as pulsation? Difficult to distinguish from 1-dimensional "vibration" in 4-dimensional vector fields, Vdiv and Vconv.

- 1-dimensional motions as vibration or linear pathway motions when halved:
   Longitudinal L-waves have in this model been assumed as the motion in 4-dimensional fields. Pressure waves within masses would be one example
   There is the hypothesis too, proposed by a scientist, about pressure waves upholding the structure and arms of our spiral galaxy. Perhaps supported by observed changes between red and blue shift in light from sources near the galaxy centre?
   Another example could be the very expansion of Vacant Space, derived from the FA -force in our model.

- 3-dimensional motions could also be identified within layers of stars as our sun, layers in a macro-scale as 2-dimensional: the convection currents as presumably 3-dimensional could be the result of the stratification into layers?

- 4-dimensional motions as pulsation, expansion/contraction in "1-dimensional structures" in cosmos? It's of course questionable if there is any sense in talking about 1-dimensional structures. They become rather abstract.
   In the case of pulsars for instance, inner processes leads to emission of electromagnetic beams in opposite directions from the magnetic poles, said to have their source in the rotational energy of the pulsar. Here the emitted beams could be regarded as 1-dimensional "structures" on a macro-scale, created by inner processes which seems multidimensional. (Hence "the other way around", from motion to structure.)
   According to scientists' suggested interpretations, the origin of these beams are also related to the angle between the axes of rotation and of the magnetic field, that's 1-dimensional "structures". The inner processes include variations in rotational velocity and sub-pulses within these, as well as assumed coupling-decoupling between core and crust. (Together surely possible to interpret as steps towards 4-dimensional motions?) (Wikipedia.)
  Why the described processes in pulsars should be limited to neutron stars, if so, is another question.

Other 1-dimensional "structures" would be what is called "field lines", if differentiated, separated through polarization processes like interference and diffraction. It feels difficult however to attribute 4-dimensional motions to individual field lines!?
   Difficult likewise to attribute such motions to spiral arms of galaxies when possible to regard as 1-dimensional structures on a macro-scale - if not as "inhalation / exhalation" through the mentioned pressure waves.

- 5-dimensional motion of 0-dimensional structures as "pole exchange"?
The very meeting point where vectors inwards transforms to vectors outwards may apply to the birth of Universe as a whole.
   If there are "black holes" where mass crashes to a point, its reasonable to think that the energy transforms to another form or reality, possibly as a suggestion here to the expansion force of Vacant Space, the opposite to Mass.
   Gravitational collapses, implosions and connected explosions, could be regarded as a secondary manifestation of such pole exchanges.

*