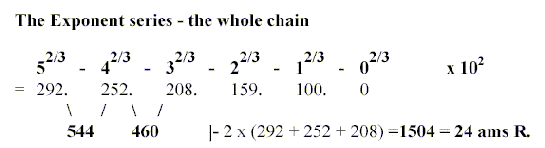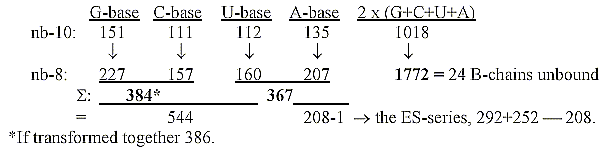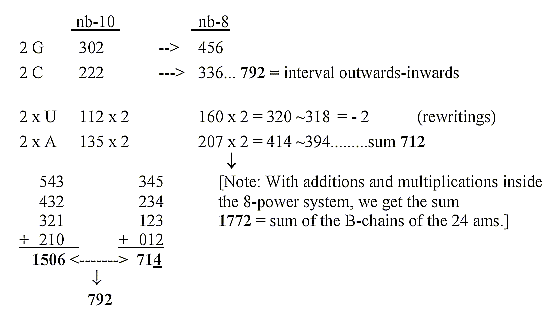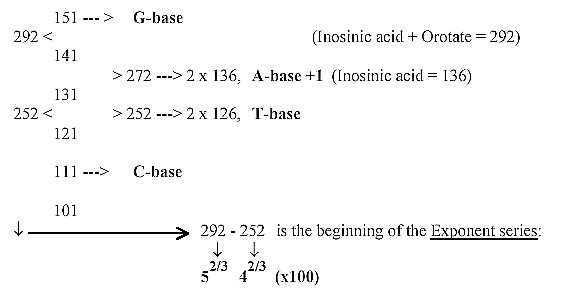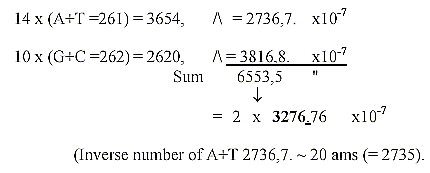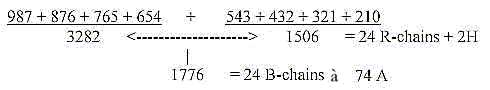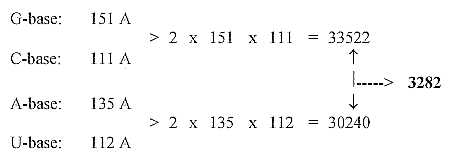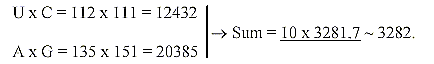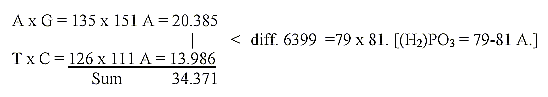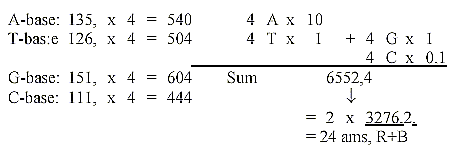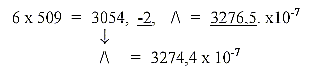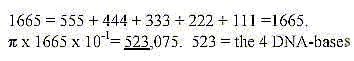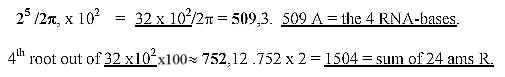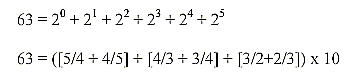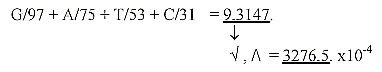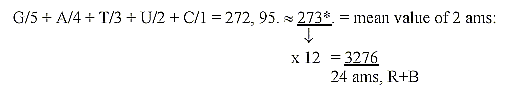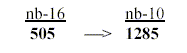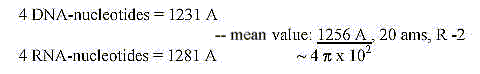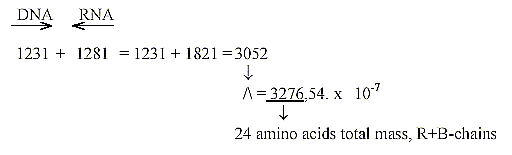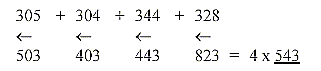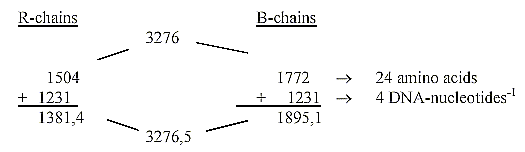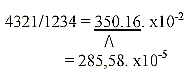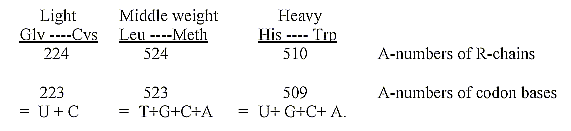Used abbreviations:
Ams = amino acids.
R-chains = the different side chains of ams.
B-chains = the similar part, which bind through condensation.
- Here it's calculated with 24 ams, the four double coded included,
where nothing else is mentioned. See table over ams here.
/\ , sign indicating inversion.
nb-x = number-base system, e.g. nb-10, nb-8 etc.

1. Two sets of the 4 bases give the mass sum of coded amino acids in nb-8:

a. The elementary number chain 5 - 4- 3- 2- 1- 0 with exponent 2/3 x10² called the ES-series:

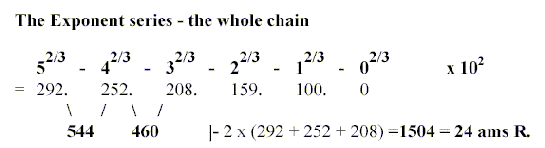
544 - 159 =385, 208 + 159 =367.

*Numbers 292-252...etc. below referred to as "5", "4" etc. elementary figures within quotation marks.

Transformations of base numbers to nb-8:

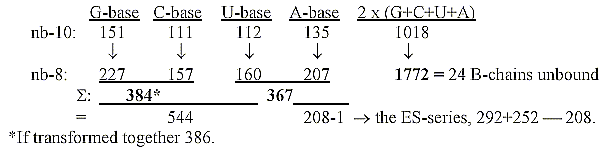
2. Division of the sum 1504 in 714 - 792-2:
Mathematical operations performed in nb-10.
   Sum of 24 ams, R-chains = 1504 divided in numbers 792-712,
related to the sums of triplets of a dimension chain through rewritings:

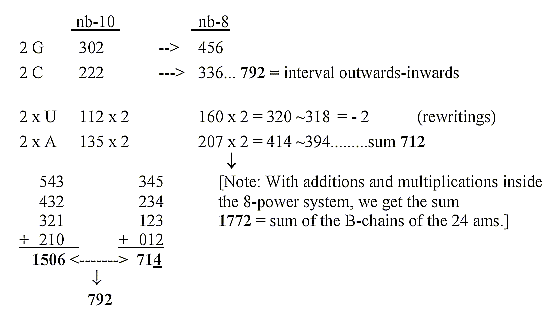
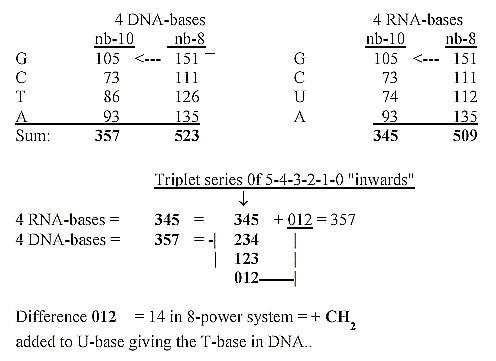
3. Mass numbers of bases read as in nb-8, separately translated to
nb-10 - and the triplets of a dimension chain:

4. Mass numbers (A) of the bases read as 6-power numbers:

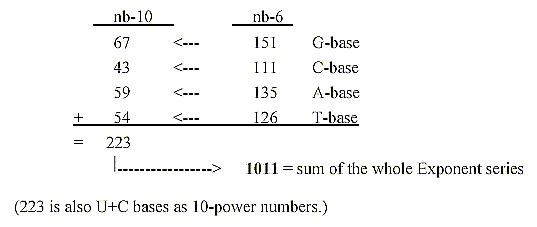
5. The bases bound with exponent 2/3 give numbers of the ES-series:

6. Middle figure in the A-number of bases as a dimension chain
between "poles" 1--1 as in the last d-degree of motions in the model:
Numbers 292 - 252 from the ES-series:

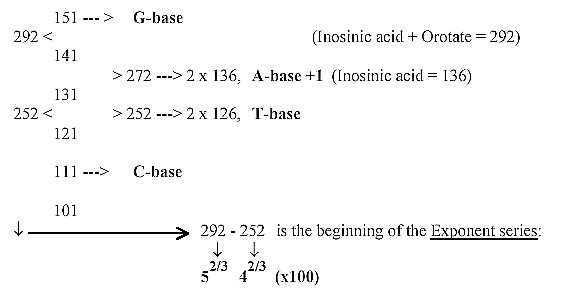
With 2 times 131 + 121 + 111 = + 363 = 655 + 363 = 1018 = 2 x 509, the sum of 4 RNA-bases. All these numbers transformed to nb-8 give the sum of the 24 ams divided 973 - 531 (as triplets of the odd-figure chain 9-7-5 (-2) —531.

Products between bases

7. Products between bases and (approximate) sums of amino acids:
Number of bases in 1st and 2nd position times A-numbers of the pairs,
inverted:

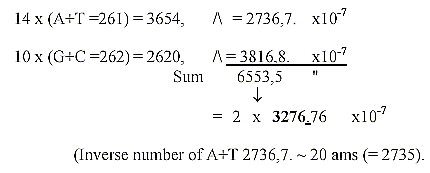
8. Products of bases and number 3282 - 3282 as an approximation?
The triplet series 543-432-321-210 expanded gives approximately R+ B-chains of the 24 amino acids:
   Sum of 24 ams, unbound, R+B-chains, = 3276: There is a loss of one H in B-chains of 4 ams, Arg 1, 2, Lys, Pro. when Arg and Lys have charged N-groups in the R-chains.
Could there eventually be a stage where there is +2H in some R-chain, giving the sum 1506? Cf. the triplet series of the dimension chain:

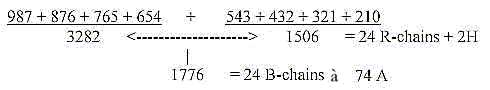
1776 = B-chains before reduction of 4 H in B-chains of Arg1,2, Lys, Pro,

Difference between base products of base pairs:

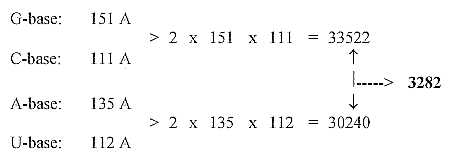
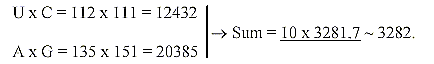
9. Products of bases DNA divided with 4 π:

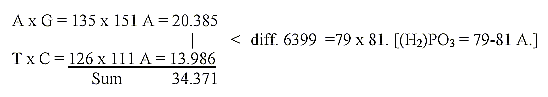
Difference 6399 / 4 π = 509,2. 509 = A+U+G+C, the 4 RNA-bases
Sum 34371 / 4 π = 2735,15. 2735 = 20 ams, R+B

Various other kinds of operations.

10. Four times the base number with displacements in the 10-power positions:

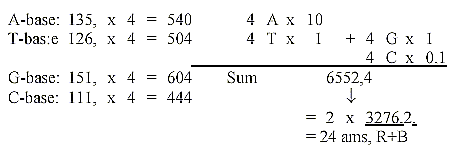
11. 24 RNA-bases, as if equal use in the codons in one position:

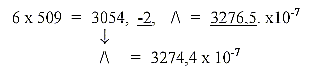
12. Natural logarithm e:

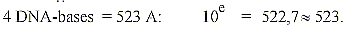
13. Dimension chain numbers as n x 111-numbers, times π:

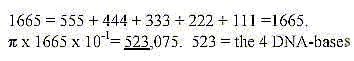
14. Number 32 and connection with the π-number?

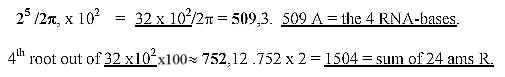
[Quotient 10⁵ / 2⁵ = 3125 → log 3125 = 3,49. Inverted ( /\) = 286,1. x 10^x.
Cf. the hypothesis in the model that 10 could be the log-base as sum of poles in d-degree 4 and 2 the log-base in polarizing direction as sum of poles in d-degree 0/00.]

15. How to show that sum of the 4 bases ≈ 31-32:

16. Number 63:

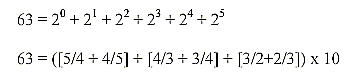
- Sum of 5 bases bound = 630 = 1/2 x 1260,
- (6,3 x 4)²= 635,04. 635 the sum of 5 bases.
- Mean value of a base = 126 A = A-number of the T-base unbound.
- Mean value for a side chain of ams ≈ ½ x 126 = 63 (62,75),
  counted on 20 + 4 double-coded ams.
- 1260 - 2 = A-number for side chains (R) of 20 ams.
- 63 = the difference A+G <—> U+C = 286 - 223.
- 63 = PO2 -group, connecting the nucleosides in DNA/RNA.

17. Bases divided with number steps,
      read in the odd-figure chain 9-7-5-3-1:

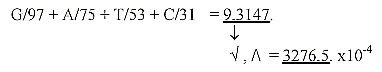
18. The 5 bases according to their mass: G-A-T-U-C divided with the elementary number chain 5-4-3-2-1:

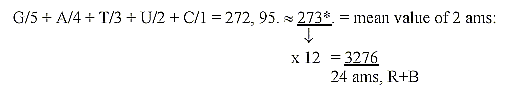
 *A+G = 286, T+U+C = 349: 286 /349≈0,819.
 819 = 273 x 3 = 1/4 x 3276, sum of 24 ams R+B

19. A more odd operation:
First figure in the A-number of the bases regarded as detached from the last figure:

Nucleotides — and mirrored numbers

20. Triplet of nucleotides in RNA with mean value 320 - 321 = ¨960 - 961:
Cf. sum of triplets in the elementary chain: 432+321+210 = 963.
960 = A+U-coded ams R.

21. The 4 bases bound = 505 give the sum of their nucleotides through nb-transformation:

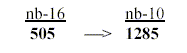
22. Nucleotides with P-groups charged -1:

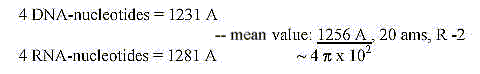
With uncharged nucleotides 1260 A: 20 ams R = 1258 ≈ the middle value.

23. Mirrored number relations?

a. Mass sum of RNA-nucleotides read backwards as in a mirror relation to DNA:

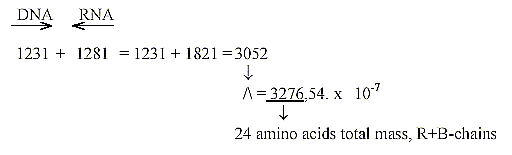
b. Mirrored numbers for separate nucleotides RNA:

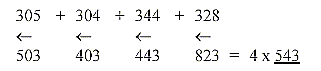
543, the first triplet number in the elementary dimension chain.
543 also the sum of the 4 bases when +2H for each double-bond in the rings are included but this concerns the 4 DNA-bases.

24. Amino acid sums, R and B chains added with displaced DNA-nucleotides:

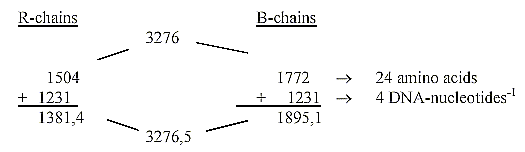
25. The four DNA- and RNA-nucleotides 1231-1281:
The sums derived from an angled reading of acidic and basic amino acids
(R+B-numbers), His included in both groups:

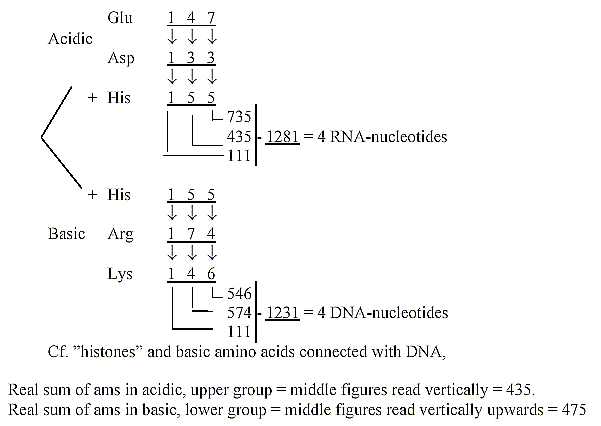
Miscellaneous other operations

26. The sums of 2 purine and 3 pyrimidine bases, 286 and 349;

a. Numbers for dimension steps "inwards" with sum of poles of next higher degree added, for instance step 4 ← 3 = number 3-4, + poles 0 and 00 worth 5 = + 10, read as 350:

b.
    

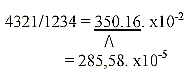
27. Division of 20 ams in accordance to their weight in three groups gives sums which -1 corresponds to grouped bases.

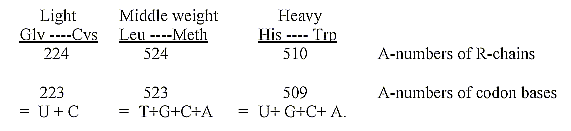
28. Numbers from 2-figure-reading and additions in the "2-figure-chain":
Example: 59 + 94 + 47 + 73 + 35 = 308 etc.

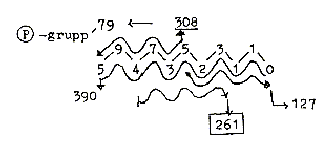
308: Mean value of a DNA-nucleotide = 307,75. (charged)
261: Base pair A+T.
127: Mean value of 5 bases unbound = 635/5- = 127

29. Mass number of the G-base 151 from inverted triplets:

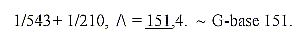
30. Mass number of C-base 111:

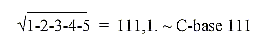
31. Rolled numbers:

*
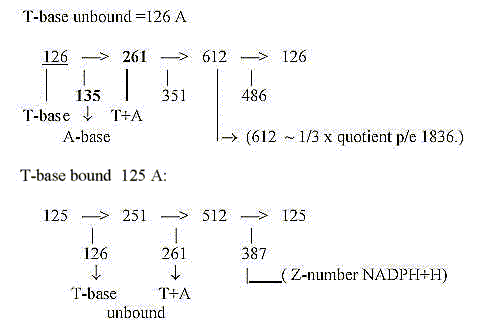