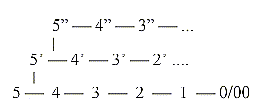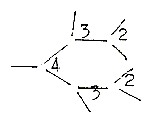Some elementary annotations:

1. 5-6- atoms in many molecules:
It could be noted that the number of atoms (C-N-O-types) on a primary level in biochemistry is about 5-6, also the number of dimension degrees or steps in a dimension chain (transformed to d-degree 1 giving 5 x 1):

- Carbohydrates as essentially C5-C6 molecules
- A tetrahedron: 5 atoms.
- A central amino acid as Glu from α-ketoglutarate is a C5-molecule.
- Start of synthesis of fatty acids as C2 + C3.
- An isoprene molecule: a C5 molecule.
- Bases: A-base as 5 x HCN, pyrimidines U-C-T: C4 + N2, a molecule of 6 ring-forming atoms.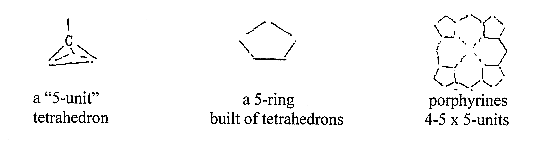

The PO4 molecule like the carbon tetrahedron with one central atom and 4 peripheral ones are fives, which may be regarded as still more elementary configurations.

(Why branching of chains after 3-5 glucose units in glycogen ?)

2. Forms of these small molecules, dimensionally interpreted:
- Tetrahedrons in relation to ring structures: 3-dimensional.
- Ring structures in relation to their own R-groups: 2-dimensional.
- R-groups of the rings in relation to different kind of bonds: 1-dimensional, as for instance the H-bonds between R-groups of the bases in DNA.

It has been said that a condition for life is the development from sp³-hybridizations in tetrahedrons to sp²-hybridization in planes, dimensionally interpreted as a step 3 → 2. Such a step towards lower d-degrees implies increasing number of movements or kinetic energy according to the main hypotheses in the model.

3. Chair- and boat-forms of d-degree 2:
The ring forms as 2-dimensional illustrate both poles 2a/2b of d-degree 2 in the dimension model, in one expression described as convex/concave, this in the "chair" form.

4. Valence numbers and division in orientation of bonds:
The divisions in directions of bonds around atoms of different valences look like illustrations of d-degree steps:

- P-atom with valence 5 get 4 bonds "outwards", 1 inwards giving one double-bound oxygen atom. A division 4 + 1.

P-group and amino acid tetrahedrons:
P: 5→ 4 + 1 (or 3 + 2, the double-bounded Oxygen)
C:          4 → 3 + 1
                     3 → 2 + 1
N:            (4)3 → 2 + 1,  (NH³⁺ 2)
O:                         2 → 2 or 1 + 1, (O^- 1 + 0 (2 in keto-oxygen, or 1 + 1, e.g. in                                                                        carbohydrates)

In ring structures in the codon bases or carbohydrates and in fatty acids there is also the division of 4 →2 + 2 or 2 → 1 +1 for R-groups: 2 forming parts of the ring or in fatty acids wavy chain structures giving 2 or 2→1-dimensional forms. Compare generally waves as expressions for more motions, lower d-degrees.

-   N-atom, when with valence 3, is in amino acids for instance or base rings divided 2 + 1 in directions and the O-atom with valence 2 has a still narrower angle between it's bond directions, 3 in double-bonds, or 1-1 in water.

5. Triglycerides divided 2 -1:
On a macromolecule level the triglycerides undergo a similar transformation step or division 3 → 2 +1, two hydrophobic fatty acids in one direction, the 3rd replaced by a hydrophilic P-group or (later) other more complex hydrophilic groups. (The fatty acids already in themselves, before binding to glycerine, polarized in hydrophobic and hydrophilic ends.)

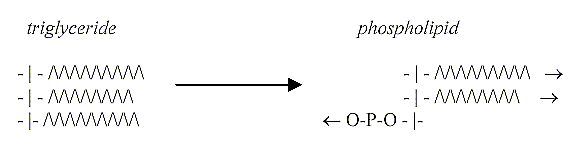
Reevaluating the lipids:
Regarding the structure of phospholipids, they illustrate in fact most obviously the 4th d-degree of directions outwards/inwards in our model - and at the same time how the d-degree 3 appears through the polarization in poles 4a -- (3) --- 4b according to the model, creating the "circular" cell membrane (with "radial" canals). Enclosing / excluding, individualizing units as cells.

6. Chains and rings as 1-2-dimensional elements building forms of higher d-degrees:
Life chemistry is processes, characterized by increasing motions, while structures of second order are of low d-degrees, chains and rings, principally d-degrees 2 and 1.
   In the dimension model the dimension chain of structures becomes opposite in direction to the dimension chain of motions, with increasing d-degree in each step outwards in structure:

                                    0/0 ← 1 ← 2 ← 3 ←  4 ←  5      D-degrees of motions
   D-degree of structure: 5 → 4  → 3  → 2 → 1 → 0/00
                                                                  |      ↓chains (proteins, fatty acids...)
                                                                 ↓ rings  (carbohydrates, nucleic acids...)

We could test to look at the relation the other way: motional patterns taking the form of structure d-degree in the opposite directed dimension chain:

- protein chains (1) moving "linearly" (1) in angular steps through 3 dimensions, when    folding to "globular" proteins, partly also spiralling (α-helixes), a 2-3-dimensional motion;
- carbohydrate chains of rings spiralling, ~ rotation (2) + pathway motions (1),  also crossed chains forming surface layers (2-3) as in cellulose coats of plant cells.

Higher d-degrees of structure are replaced by motional patterns as a substantiation of kinetic energy. 3-dimensional forms on this level are only created through motional patterns:

It could perhaps be one way to interpret the folding of proteins?
   (Following internal bonds between different parts and the aggregation to dimers and tetramers possible to regard as expressions for the 4th d-degree, e. g. in histones and enzymes?)

7. Displacements in carbon chains at additions of other ones:
Displacement steps in the connection between "C-atom-lines" of the included units seem in many cases to be a factor in the formation towards units of higher d-degrees:
   In such cases the added unit don't bind to a C-atom at the ends of the other but to the second one or the like:
- One obvious example is when two δ-aminolevulinic acids (C5 molecules) combine to porphobilinogen, where the 3rd C-atom in one of the molecules binds to the 4th in the other, leading to the creation of a 5-ring.
- Another example is the connection between acetyl~ and dimethylallyl(-P-P) molecules on the way to mevalonate and isoprenes.
- Also the coupling of acetyl~ to middle C in malonyl~ at the synthesis of fatty acids.
- The fact that it is the oxygen group of the second (an inner) C-atom that is replaced by an N-group at amination of α-ketoglutarate to amino acid Glu could illustrate the same principle?
   Such features could eventually be interpreted as expression for primary versus secondary development within a dimension chain:

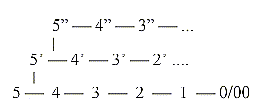
8. Formation of rings in 5-6 types:
Forms of molecules "of second order", combined smallest molecules, are chains and rings, i.g. d-degree 1-2-(3). (Eventually connected with step 1-2 on the atomic level, the p-orbital, to which the C-, N-, O-atoms belong?)
   There seems to be at least 5 quite different types of ring formations, as if "every tool" for the purpose of ring-closing were used. They are however more or less connected with the different main classes of substances and perhaps but not easily possible to interpret as formations in different d-degrees in the model, in a secondary dimension chain developed within step 2 →←1. ?

The step from tetrahedrons with central atoms to ring-formed molecules (cf. sp³ → sp²) may be regarded as a projection of centre to anticentre, to a circumference, as of the 6 edges in the tetrahedron; a displacement to a new level, a level of lower d-degree.

According to general hypotheses here a whole dimension chain may also close stepwise towards a ring form through angle steps if in the same direction.

Figures below are only vaguely suggested associations with geometries of the different d-degrees, surely debatable.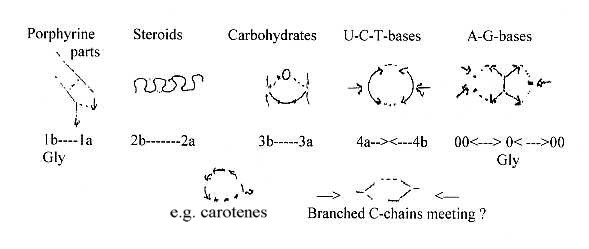

a. Porphyrine synthesis with two nearly parallel or anti-parallel C-chains who through side bonds form 5-atom rings.

b. Synthesis of steroids where the wavy chains (of squalene) give closed rings in both directions, convex/concave as poles 2a-2b of d-degree 2.

c. The simple bending of the C-chain (3a) in carbohydrates bound as through radii (3b) from an O-atom as centre, a loop formation.

d. The meeting (opposite directions as 4a--4b) of two bent C- and or C-N-chains forming "half circles" of a ring as in the creation of the pyrimidine rings,U-C-T-bases.

e. Creation of double rings as in purines (A-G-bases) from a "radial" centre (0) (there the amino acid Gly, a tetrahedron) and a multitude of small individual molecules meeting from outside (00) supplementing and completing the ring forms.

Theoretically 3 steps of bifurcations can give a 6-atom-ring.
To compare with 3 polarizations from d-degree 5 to 2.

(The interpretation of the ring forms belong to the many ambiguities in the dimension model. A molecular ring may be interpreted as a surface, d-degree 2, further as a circumference (pole 3a of d-degree 2) or as a secondary, complex centre on a superposed level as in the many ring-formed coenzymes in relation to the surrounding globular protein enzymes, Ep.)

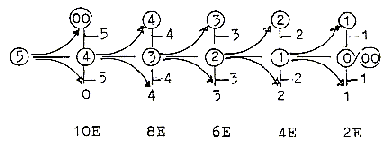
9. Z-numbers of most elementary molecules in a "10-chain":
Number 10 stepwise polarized, giving OH-H, O-H2, N-H3, C-H4:

(Abiut the Citrate cycle: In reality there seems to be - 5 H from substances/molecules in the citrate cycle. If 8 H are gained to the respiration cycle, 3 of them ought to come from outside during the circle…?)

A level development within step 3-2 .

The "10-chain" may be regarded as a doubled elementary dimension chain with its two polarizations 5 → 4 + 1, 5 →3 + 2.
    9-1, 7-3 in that case as partitions in the half steps 5 → 4, 4 →3.

H-atoms = the d-degrees which are lost during the stepwise process towards lower d-degrees, translated into movements. Compare H+ as an essential "force" or "carrier of force" in biochemistry.

2 H = "2 E", E for the sum of poles in respective d-degree, a kind of energy value in this model. Total sum of a dimension chain give sum of poles = 30 "E".

*