|
The 5-dimensional model
is here applied on plants with aspects on mostly
rather elementary data. Plants show more clearly geometrical features
from the model in their different kinds of polarities.
1. Numbers and fundamental directions in angiosperms:
Angiosperms are classified in two main groups with distinct
features: the one with 2 cotyledons or seed leaves (dicots), the
other with 1 cotyledon (monocots). The dicots are 5-4-numbered in
flowers, the monocots are 3-numbered, often 2 x 3, in their flowers.
Cf. the elementary dimension chain 5-4-3-2-1-0 less developed
as 5 - 4 - 3 - 3 or 5 - 4 - 6.

Fig
Pl-1-163-1
All plants follow a "numerical plan" based on numbers 5, 4, 3 and
multiples of these (Ps p.56). for instance 4 sepals, 4 carpels,
4 petals, 8 stamens, called a "4-merous" plan.
If amino acids and the genetic code can be derived from a dimension
chain through the "exponent series", it would be natural to find
corresponding number relations on superposed levels. The recurrent
number 5 should have a foundation. In this "exponent
series: x^2/3 x 100, (x = 5-0)
the mass of G- plus C-coded amino acids (side chains) are derived
from numbers 5 and 4, and the difference to A- plus U-coded amino
acids is derived from number 2 x 3; cf. 3+3 petals, 3 + 3 stamens,
3 carpels is the basic type in plants with 1 cotyledon.
Compare also the Balmer series for spectral lines of hydrogen
, within the visible area, m
= 5, 4, 3 and n = 2 (introduction).
It’s also meant that direction of evolution has been the one from
plants with 2 to plants with 1 cotyledon - or eventually that both
types derive from a common, preceding type most like the dicots
(Sb). It sounds natural looking at the figure below: the
single cotyledon seems as a "halving", as out of a polarization
in terms of the dimension model:
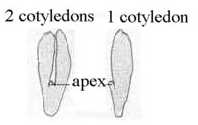 Fig
Pl-2 (after picture from reference Ps, p. 78) Fig
Pl-2 (after picture from reference Ps, p. 78)
Compare however the ambiguity in reading of the dimension chain,
straight outwards or as in the loop model: debranched degrees from
higher steps meeting the other way around, in synthesizing direction:
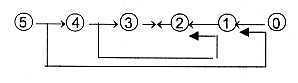 Fig
Pl-3 Fig
Pl-3
[Number of dicots nowadays is said to be about 3 x 55.000, number
of monocots about 1 x 55.000: a quotient 3 to 1, as (5 + 4) to
3, although it’s hard to believe in a connection and the estimation
of numbers must be very uncertain. Other figures exist.]
Roots differ between the two main classes of plants:
Primary root in dicots goes vertically downwards and becomes
the main root. This is the primary coordinate axis of the plant
outwards – inwards as poles of dimension degree (d-degree) 4, on
the physical level corresponding to forces.
FA of expanding Space, (here defined by sunlight)
and FG , gravitation towards Mass.
In monocots this root disappears and gets replaced by "radial"
adventitious roots, which can be interpreted as a d-degree
step 4→ 3. These roots originate
also from the lower part of the stem, that’s from the upper
side of the seed, from the pole 4b of d-degree 3 in our model,
representing outward direction, leading to radial structure in next
step. Although, as through mixed with the opposite pole, now inwards.
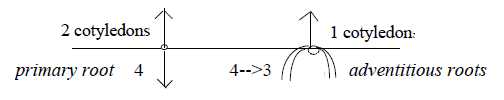
Fig
Pl-4-163-2
Growth of woody plants with 2 cotyledons is both lengthwise
and horizontally radial, called secondary growth of thickness; in
plants with 1 cotyledon it's only lengthwise, called primary. In
directions outwards in a dimension chain it implies a reduction
in d-degrees from dicots to monocots, which seems supported in the
evolution (?). The terminology suggests the opposite direction.
Dimensionally it corresponds to an additional step 4→> 3 in coordinate axes (about cambium below) and implies
anyhow a higher potential of development. (Cf. about animals in
file Evolution,
No. 7.)
Vascular, conductive tissue has a cylindrical or net-shaped
character in dicots, while it gets split up in strings in monocots
(see further below).
Other corresponding features are that leaves most often
are outspread sheets in dicots but become more linear, band-shaped
in monocots ((in macro-shape as a d-degree step 2 → 1, and venation is branched in dicots, mainly unbranched
in monocots - a development towards the linear form also in this
aspect.
2. Main polarizations of directions:
 Fig
Pl-5-166-1 Fig
Pl-5-166-1
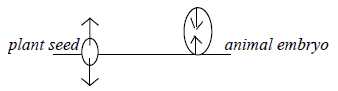
Plants develop, animals "invelop" or involve themselves.
Seed of a plant growths outwards from both its poles, while
the animal embryo
growths circular and inwards through invaginations from its poles
(in a "negative curvature").
That’s by no means the whole truth but yet a fundamental opposition.
Outward – inward directions as fields of d-degree 4 corresponds
also to a 0-00-polarity and the relation between an underlying and
a superposed level. It’s the relation too between plants and animals
living on plants.
It’s said that a special radial polarity can be reversed in plants
by certain chemicals as for instance ethylene: adventitious roots
can grow inwards the stem center instead of outwards. Are there
perhaps similar substances that are decisive for the polarity
plants – animals, besides chlorophyll and the photosynthesis?
From Succinyl~(CoA), when it leaves the citrate cycle, the process
goes to creation of porphyrins together with the amino acid Gly.
These porphyrins have a center - anticenter structure
that may illustrate d-degree 0/00 in
our model and represent a crossroad and division of ways to chlorophyll
of plants and hemoglobin in animal blood.
Roots usually lack pith - also in this respect characterized by
inward direction, lack of a center.
A comparison in directions between pines and firs
could illustrate the d-degree step 4 →
3 and following steps as halvings:
- Pine: main root vertical; new shoots vertical;
paired needles, arranged in a circle, and long.
- Fir: root branched along the surface of the ground;
new shoots horizontal; needles unpaired, in half circles and short.
3. Symmetries of flowers:
Symmetry planes from many to one:
Many planes ————>
2 planes ———>
1 plane
Radial symmetry ——> Bisymmetry
——>
Zygomorphic
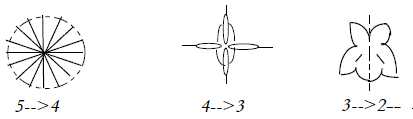 Fig
Pl-6-164-1 Fig
Pl-6-164-1
Radial symmetry implies a shape of the type vector fields between
center and anticenter as out of d-degree step 5 →
4 in our model (in plane projection).
The bisymmetric shape exists in 4-numbered cruciferous
flowers. Two perpendicular coordinate axes have been assumed in
the model to follow from d-degree step 4 →
3
Zygomorphic shapes are for instance labiates and
flowers resembling butterflies.
The earliest flower plants (mostly represented in gymnosperm class
Bennettitatae) had open flowers with radial symmetry, and
early fossils of angiosperms show that these too had mostly flowers
with open, radial symmetry (Sb p. 128).
Hence, a development should have occurred from
more symmetric to less symmetric, more irregular flower shapes.
(Cf. the development from early radial-symmetric
1-2-layer animal organisms
to lateral bisymmetrical ones as worms or fishes.)
Radial-symmetric flowers exist both with and without terminal flowers,
while those with only 1 symmetry plane don’t have terminal flowers.
In the inflorescence it implies a transition from the vertical axis
up - down to the lateral axis as a dimensionally later step.
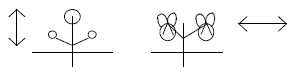 Fig Pl-7-164-2 Fig Pl-7-164-2
(See further No. 8 below about inflorescence.)
The development of more irregular flowers as labiates, tube-shaped
ones and those with spurs and such shapes came later with other
types of insects. The growing together of petals to more or less
closed rooms could be the result of the inward directed force, one
pole of d-degree 3, the degree of volumes. Cf. cotyledons that get
the form of tubes in monocots.
In the differentiation of petals it’s often possible to observe
the division 4 – 1 or 3 – 2 of number 5 as in the loop version
of the dimension chain:
(Three steps of polarizations: 5 →
0/00, 5 →
4/1, 5 →
3/2; an angled reading of the
chain.)
We can note that in labiates for instance, its
the upper lip that has 2 lobes, the lower one 3
lobes, positions corresponding to the views here on higher degrees
and numbers as the deeper, lower ones, lower degrees as the more
superficial ones.
4. Conductive tubes:
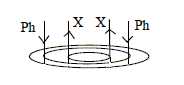 Fig
Pl-8-166-2 Fig
Pl-8-166-2
- Transportation of water and salts upwards goes through
tubes called xylem (X), transportation of carbohydrates and
other synthesized substances goes downwards in tubes called phloem
(Ph); synthesizing direction = inwards toward higher d-degrees in
the model. (About molecules, cf. a figure about "A-Z"-numbers
of chemical elements.
Outward direction in the dimension chain means increasing entropy.
The transport of water upwards in the vessels occurs mainly through
vaporizing as the main driving force and doesn't demand energy.
In terms of phases
it implies a d-degree step 2 → 1,
liquid to gas phase. In the opposite downward = inward direction
the transport demands energy, i.e. in direction towards higher d-degrees.
(It may contradict our feelings of gravitation, the FG-force,
yet the direction of Space outwards, the FA-force,
dominates plants.)
The general arrangement of xylem and phloem in dicots illustrates
very clearly the general principle in the model: outward direction
from center, the 0-pole, inward from the anticenter, the 00-pole.
It seems defined by at least 3 polarities:
1) center – anticenter in cross section : ac → ↓
and ↑ ← c
2) direction of transportation up/down,
↑ ↓ and
3) stem – root directions.
Xylem with upward transport is arranged in an inner ring, phloem
with downward transport in a peripheral one, a center – anticenter
polarity.
Further, at creation of the primary tubes
in the stem, phloem (Ph) is constructed in inward direction and
xylem (X) in outward direction (Fb): ac →
Ph | X ← c.
In the root however, both kinds of primary vessels
are created from outside inwards, which appears as decided by the
polarity stem – root and inward direction of the root becoming dominating.
Roots lack pith and thus their vessels come to make up the center.
Monocots have as mentioned above only the primary growth of thickness,
while among dicots the secondary growth of thickness
develops from an intermediate layer, the vascular cambium,
between xylem and phloem, which can be compared with mesoderm in
animals.
In cross-section the tissue layers between surface
layer and pith grows both radially and circularly, which gives the
annual rings with increasing amplitudes, according to the geometries
in d-degree step 3 – 2.
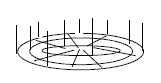 Fig
Pl-9-167-1 Fig
Pl-9-167-1
From the vascular cambium the directions of growth of Ph and X
gets reversed:
ac ← Ph | X →
c, Ph outwards, X inwards., It retains the relation of positions
(ac- c) as obviously more fundamental.
Cf. the secondary center in step 3-2 in the "haploid"
version of a dimension chain:
(0 →4→
3→ c2 ←
2← 1← 00).
to compare with development of mesoderm or cambium from which we
get outward direction. (The same concerns coelom in Deuterostomia
animals.)
Arrangement of xylem and phloem according to illustrations (Ps
p. 75) the inner xylem have a tight, radial structure, the
ring of phloem a scattered, fragmented circular structure of vessels
in cross-section, showing the geometrical polarity radial - circular
poles of d-degree 3 in our model but also the one of unity versus
multitude between 0- and 00-poles.
The radial and circular growth of thickness becomes
a growth in d-degree 3 in relation to lengthwise growths of d-degree
4, up-down, when it concerns the main coordinate axes.
The fact that cells of xylem become hollow
and dead in forming the canals while cells of phloem are living,
even if lacking nuclei, may surely be explained in terms of good
function, but could seem to contradict most other dimensional views
in these files.
However, there is the opposition Space versus
Mass, the FA-force up-/outwards
of Space and down-/inwards of Mass, and
the FA-force is the one characterizing plants,
unquantified direction from 0-pole and unity. From this aspect the
cell death in xylem could be described as a return to the deeper
vector level where the property of mass disappears and where the
conducting canals are just vector fields. (That centrioles
in the inner of a cell of the type 9x3 + 0 is perhaps a related
fact?)
The alternative view on xylem, in the other direction,
is that the shapes of cells transform to lower d-degrees outwards,
become 2-dimensional tubes, 1-dimensional conductive canals on a
macro-scale, and in last step only is transportation, vectors for
motions, d-degree 0/00.
When it concerns transported media, water represent naturally a
phase of lower d-degree than synthesized carbohydrates in phloem.
.It represents steps in phases from liquid to gas phase (vaporizing
of water the driving force upwards in xylem) and further to the
division, the polarizing of water and a "plasma phase"
in the elevation of electrons in photosynthesis. (In contrast, direction
inwards implies steps towards phases of higher, substantiated d-degrees.)
The cell types for phloem and xylem are said to
originate from differentiation of cells at apex of branches – furthest
out, corresponding to 0/00 in the dimension
chain. Cf. that outer poles of d-degree 4, the one of vector fields,
meet in d-degree 0/00 of motions.
(What to call the phase of emptiness?)
Steles:
There is a theory about the historical evolution of the conductive
tissue in plants. (Fb p. 80). That evolution resembles an
illustration of features in a dimension chain:
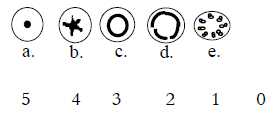 Cross section: Fig Pl-10-168
Cross section: Fig Pl-10-168
Figure freely from the source;
- a) center – anticenter polarization as in a step 5→
4, the "protostele":
a central xylem surrounded by phloem. Is found in first land living
plants,
b) a radial field of directions as a step 4→
3b, the "actinostele":
xylem becomes star-shaped with ridges that divide the surrounding
phloem. Is found in the stems of very old fossils of land living
plants.
It's also the type of stele, the "radial conductive
string", found in all ferns and in roots of seed plants. Actinostele
are typically 'exarch' with xylem growing inwards.
Perhaps that's a reason why the roots - growing inwards
- of vascular plants normally are considered to have exarch development
(Wikipedia). (In opposition as it seems to endarch
xylem that grows outwards, said to be typical for stems
of seed plants.)
c) a circular, cylindrical form as in a step 3a→
2, the "siphonostele":
xylem in a close cylinder, its outside covered by phloem. Its shape
is assumed as resulting from a developing pith in the center, hence
a kind of center displacement outwards.
d) division of the circular ring as a (partial) step
of polarization 2→ 1, the "dictyostele":
gaps in the closed cylinder.
e) a splitting up of the cylinder to separate strings,
as a last step 1→ 0/00,
the "eustele": each string composed of inner xylem, outer
phloem.
It is assumed that the type of stele in stems
of monocots, called "atactostele", with its spread strings
– as ‘points’ in a macro-scale – possibly can be derived from this
eustele, which in that case should agree with the other dimensional
features of the step from dicots to monocots as a kind of halving.
Number of tubes is also a differentiating feature among
plants. Botanists distinguish between plants with 2 – 3 – 4 - 5
…etc. tubes, which seems as a principle of division agreeing with
views in the dimension chain as numbers.
5. About two other polarities between species of plants:
Transversal polarity of directions within structures of
flowers are said to have a big systematic value for classifications
among plants.
One distinction is made between plants where the
seeds grow peripherally from enclosing walls of carpels and those
whose seeds grow from the middle, the center; hence, a center –
anticenter polarity, the complementary poles out of d-degree step
5 → 4 in the dimension chain.
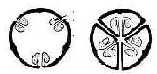 Fig
11 from reference Sb Fig
11 from reference Sb
However, there are more clear examples of central ovules than in
the right figure above, where carpels are folded radially inwards
and ovules develop as from the center their borders define. (Cf.
d-degree 4a in the model and last step where motions to each other
define a new 0'-pole. In fact, it resembles also how material growths
from the animal pole in an animal embryo
and invaginates at the V-pole.)
An example of plant with central seeds is the
5-numbered sticky catchfly and an example of anticentral
seeds is the 4-numbered crucifer family. It’s in notable
agreement with the dimension model when numbers are read as expressions
for d-degrees: the relation higher to lower d-degree, here 5 to
4, as a relation center – anticenter.
Among plants with numerous stamens a distinction is made between
those where the stamens are formed from inside outwards, centrifugally,
and those where the stamens are formed centripetally, from outside
inwards. Hence, a counterpart to the distinction of seeds above.
Cf. the similar distinction between prokaryotic
and eukaryotic algae: in prokaryotic algae the cell wall at cell
division is formed from outside inwards, in the eukaryotic ones
from inside out (Fb s. 31).
Apical growth versus lateral growth, mentioned above:
Coordinate axes as expressions for d-degrees: the 4th vertical,
the 3rd lateral:
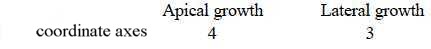
Fig
Pl-12-169-1
See further No. 8 below about inflorescence.
Coniferous trees and certain broadleaf trees have a principally
indeterminate apical growth upwards along the vertical axis. In
many broadleaf trees however, especially deciduous trees, the apical
main shoot dies in each branch generation and it is the lateral
shoots that grow and develop.
Note that gymnosperms as conifers are earlier
in evolution and we get an evolutionary step d-degree 4 →
3.
Cf. that early plants with radial symmetry have
top flowers, not the later irregular, zygomorphic ones.
An indication of the qualitative difference – as through a quantum
jump – between the directions designated "4" and "3" is that the
same chemical substance, auxin (from the amino acid
Trp), have different effects vertically and horizontally: promotes
the vertical growth of apex but impedes the growth of lateral shoots.
Impeding chemical signals from the apex increase
also the angle of lateral shoots towards 90°. In
the dimension model the inward direction (pole 4a) is a primary
polarizing force and outward/inward directions
transform to a perpendicular relation in step 4 →
3: 180° → 90°.
(It reminds of the similar function of human
brain where most motor signals from cortex, ~ "the top",
seems to be of the inhibiting type.)
The horizontal position of leaves can probably be interpreted as
a result of one "anti-gravitational force" (Fb) upwards and
a downward directed force, expressed in the stronger content of
auxin on the upper side of leaves. It’s an interesting introduction
of the FA-force
from expanding Space in macrocosm into the upward growth of plants.
It’s also in agreement with how the 3rd dimension is
generated as complex result of the poles of d-degree 4 in the dimension
model here.
 Fig
Pl-13-169-2 Fig
Pl-13-169-2
About ferns it’s said that most of them have a top cell
that first through 4-sided division become the meristem cells,
which in their turn divide 3-sidedly in the shoot, hence a step
4 → 3 in the very process of divisions.
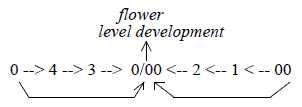
6. Evolution of seeds and flowers:
A relation between conifers and flowers, an illustration:
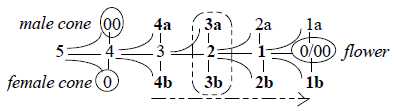 Fig
Pl-14-172-3 Fig
Pl-14-172-3
Male and female seeds of cones spread by the wind, united in a
flower.
A flower in relation to a developed plant: illustrated
by d-degree 5 developed through following steps in a dimension chain
in relation to last "d-degree 0/00", equivalent
with 5’, where new poles 0’ and 00’ are defined: a substantiated
start for new individuals. In a level chain it’s the single cell
level, compared with the contact and tissue levels.
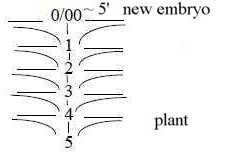 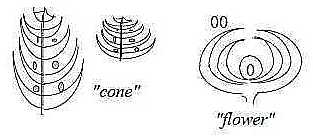
Fig Pl-15-170-1-v, Pl-16-172-1-h
A d-degree step 1→ 0/00
is however represented in every step outwards in the
dimension chain, at each polarization (ramification), like seeds
on cones of conifers.
Theories about the development of seeds:
It’s believed that conifers originated from a duplication
of genome, which led to a polarization between micro- and macrosporangia
that became separated on different cones or even on different individual
trees. Through a new polarization – "meiosis" – it led to a haploid
phase and fertilization through wind-carried pollen. It sounds as
a series of "polarizations" on different levels. (Cf. Genetics.)
How the complementary, sexual polarity arose from
simple cell divisions isn't explained but seems to presuppose a
small, unrecognized difference between two "daughter"
cells at each division, stepwise - or suddenly? - growing to complementarity.
The "telom theory" can be said to concerns a
still deeper level.
Telom is the simplest type of branching in vascular
plants, the Y-form (Sb p. 99) , hence of the type
2x. According to this theory germs to seeds in seed
ferns should derive from a lateral meeting between such teloms
(Sb).
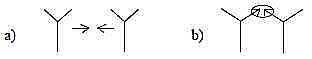 Fig
Pl-17-173-2 Fig
Pl-17-173-2
The thought seems to be that meetings between equal, potent
cell tissues give rise to a new level of development. The theory
resembles how germs to fruits, the ovules, develop at borders where
carpels meet.
Cf. meeting leaves defining a border: d-degree
2a-1-2b in our model and last step 1→
1a/1b and 0/00
in our model, where "motions to each other" define a new 0’-pole. It's
a meeting between opposite directions.
In the dimension model it’s assumed that a meeting
between two similar units (of type dimension chains) is necessary
for a development of a new level. Only two similar
units with outward direction from a 0-pole give such a meeting;
mutually they become complementary. O—>
| <— O. Two equal units become each
other’s anticenter. Yet, a secondary factor seems necessary to presuppose
that leads to the polarity macro-/microsporangia
Stamens in flowers are probably transformed petals (Sb
p. 158) according to a more common belief, stamens and petals
are understood as homologous organs. In macro-shape it’s a relation
d-degree 2 – 1, cf. outer poles of d-degree 1 = 2a, 2b: 2a –
1– 2b, which may confuse the interpretation.
It seems that it could be an example of the same
telom theory. Stamens defined at meeting of petal edges (?), left
figure below. Right part of the figure illustrates a similarity
with how seeds are arranged in certain ovaries, as at the edges
where carpels meet?
 Fig
Pl-18-173-1 Fig
Pl-18-173-1
Theories about emergence of flowers:
A flower corresponds according to certain hypotheses to a shoot,
i.e. stem and leaf parts, however not quite so (Sb p. 126 f.).
Flowers have also germs of roots, which shoots seems to lack as
they are described (?). It’s said as a fact that the female cone
of conifers is a branched shoot, part of the trunk with leaves.
If so, it would lack a germ to roots! Retrieved in the male cone?
Cf. inward direction of roots and in male gametes?
Three theories share the hypothesis that anticenter just folded
around a center (expressed in terms of the dimension model):
- that the leaf carrying seeds just folded and closed along
its edges to form a wall around what became the pistil.
- that stalked microsporangia on leaves in a circle below
upper small branches with germs to seeds came to grow up and close
around the seeds; upper leaves becoming carpels, the lower ones
with microsporangia becoming stamens and formed the perianth (Sb,
p. 127). Or
- that in groups of macrosporangia the central became germ
to the seed (nucellus) and surrounding groups became the coverings.
Hence, what becomes the seed would be defined by the position,
a simple geometrical circumstance (similar to the one between vascular
tubes phloem and xylem, originating from polar cell types at apex
of branches).
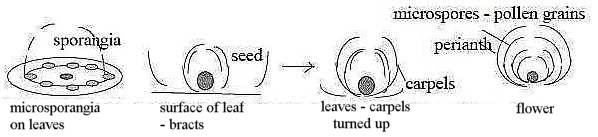
Fig Pl-19-171-3
In outer form it implies a step inwards from a plane arrangement
of d-degree 2 to a closed form of d-degree 3. Simultaneously a force
behind the folding seems presumed, as a convergent vector, pole
4a in our model, transformed to a circular geometry versus a radial
center (macrosporangia on twigs? - as in a d-degree step 4 → 3.
Yet, it sounds unlikely that such a process simply
should take place on spread out leaves. The development must presuppose
a jump on the genetic level. Cf. a dimension chain as "haploid",
0 →> 4 →>
3 →> ←
2 ← 1 ←
00, where the 00-pole of d-degree 4 is debranched and meet
"the other way around" in inward direction:
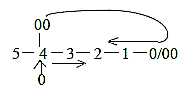 Fig
Pl-20-005-1 Fig
Pl-20-005-1
An associated but alternative theory (Sb) about origin
of flowers is that these derive from a preliminary stage in development
of a seed where the inner leaves remained folded. It’s the kind
of theory called neoteny (Sb p. 127) where a new kind
of species starts from an earlier phase of embryonic development
of an earlier species. (Cf. the thought that human beings derive
from the similar embryo stage of the anthropoid ape.)
In positions, conifers have seeds directly
on leaves as lateral and in shapes 2-dimensional, while flowers
appear directly on the top of main axis or branches as on d-degree
4 or 3 with both ovulum and petals/stamens.
It could be interpreted as a difference in levels:
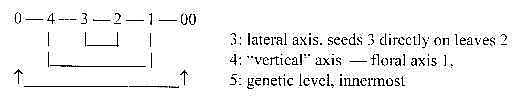 Fig
Pl-21 Fig
Pl-21
In this sense a kind of neoteny.
Hence, flowers of angiosperms seem to derive from a deeper, virtual
level.
Cf. the theory that flowers derive from "shoots",
at an apex.
In outer shape, however, a flower in itself can be described
in d-degrees 3 - 2:
Ovary is a room, d-degree 3, with
the female reproductive cells and comes to include the nourishment,
~ mass, from the polar nuclei that fertilized become triploid.
Stamens derived from petals, d-degree 2.
Simplified to d-degrees 3-2-1-00:
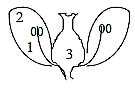 Fig
Pl-22-173-3 Fig
Pl-22-173-3
3: ovulum – 2: petals – 1: stamens, filaments – 00: pollen sacs
The development regarded according to the loop version of a dimension
chain:
 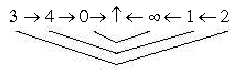
egg -----.. ovary ------ petals - stamens - pollen............chain turned inside - out
Fig Pl-23-172-2, Pl-24-172-2b
From center outwards in a flower there are 5 –
6 "layers" or steps of concentric structures:
embryo sac – integument – carpels –|– stamens
– petals – sepals.
——————————> —————————————
seed of conifers.............................angiossperms
 Fig
P-25-171-1, A seed of conifers with integument Fig
P-25-171-1, A seed of conifers with integument
- Integument is created from inside the seed outwards.
- Carpels = "fruit leaves" become part of fruits, cf. mass in
d-degree 3.
- The steps 2-1-00 in the figure become turned in the other direction
00 ← 1 ←
2
Structure versus motions characterizes the
polarity female pistil– male pollen in agreement with the directions
from 0- and 00-poles in the haploid version of a dimension chain.
(D-degree of motions increases with decreasing
d-degree of structure outwards in the dimension model. Structure
and motions
become opposite dimension chains.)
Male reproduction cells show the inward direction
from 00-pole (the pollen tube one expression) and become characterized
by movability. While corresponding female cell shows
the outward direction from a 0-pole only in its structure,
in the upward directed style of the pistil.
In general terms the evolution is naturally of the
same kind as in the animal kingdom to more and more enclosed embryos.
It illustrates also the general principle of a stepwise building-in
of the 00-pole (fertilization being just a primary example), which
is one way to express the condition for further differentiations.
7. The cell level: Cell divisions to eggs and sperms:
In higher plants the female reproductive cell divisions is similar
to the one in animals but goes further. It divides first two times
to 4 cells = 1 + 3;
- 3 cells "disappear" – or perhaps just get "immaterialized" into
vector fields of d-degree 4? (Cf. Genetics,
last No.). In plants the remaining cell divides three times to 8
cells.
- These 8 cells get positioned 3-2-3 in the ovulum, cf. d-degree
2 and its outer poles in the dimension chain below: 3a - 2 –
3b:
3 antipodals — — 2 central polar nuclei —
3 cells at the opposite end = 2 synergides
plus the egg.
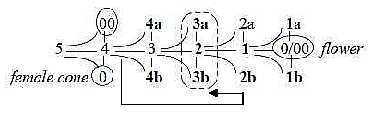 Fig
Pl-26 Fig
Pl-26
It seems that we could regard the one cell that develops further
as represented by the step 4 → 3
in dimensional terms.
Cf. the loop model, where step 4 →
3 (+1) outwards corresponds to step 2 ←
1 inwards: As mentioned above the 2 polar nuclei (eventually fused)
become triploid after fertilization by one of two sperms.
On one level in he cell we have simultaneously three polarizations
from 5 to 2 or from 0/00 to 3, in the
2x-series giving 8 cells.
The male reproductive cell follows first the simple
2x-series: 1→ 2→
4→ 8 but in following step within
the pollen grain a complemntarity appears here too, with one "vegetative"
cell that don't divide, one cell that divide in 2 sperm cells, thus
giving a 3-cell male grain.
The "pole meeting" from center and anticenter
respectively becomes indeed complex. Just one further note:
Since one of the sperms fertilize the polar bodies
in ovulum, one the egg, they seem obviously to be complementary
in some respect - like poles 2b - 2a in the figure above?
Opening of the ovule has different angles, which becomes
a secondary distinction between species (Ps p. 77): vertical,
horizontal, oblique as 180° →
90° → 45°,
a general feature hypothesized in the model when the dimension chain
is regarded in terms of angle steps, halvings of a whole circle.
Function of the antipodals doesn't’t seem known:.
They obviously mark a main "vertical" axis in relation to the egg
with synergides, hence a kind of axes 00 ← →
0.
One question is if they perhaps have some influence
on the development of a first sector division within ovary, a central
axis of tissue to which central ovules are bound in flowers with
seeds from center?
Another hypothesis could be that they have some
guiding effect on the surrounding of the ovary, right through its
wall, on petals and stamens and their circular growth? (Compared
with the cell material at animal pole of animal embryos.)
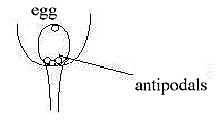 Fig
Pl-27 Fig
Pl-27
On the deep, underlying elementary level of physics the inward
direction (pole 4a) is the FG-force of gravitation,
the outward direction the FA-force (pole 4b)
of expanding space.
In a more narrow sense the two forces could be re-found in
flowers:
a) Inwards from 00-pole, fertilization of egg and mass growth through
nourishment.
b) Outwards from the 0-pole: fruits splitting up – seeds spread
– disseminated.
Like contraction to stars and fusion, "disseminating" fused matter
and sometimes explosions to new cycles.
8. Inflorescence– foliation– leaf forms and venation:
Some sketched descriptions of the variation with aspects from the
dimension chain; not unambiguous and not a foundation for any systematics.
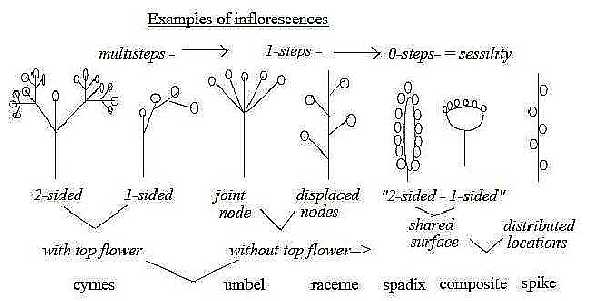
Fig Pl-28-174-1
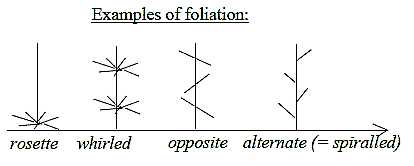 Fig
Pl-29-174-2 Fig
Pl-29-174-2

Fig Pl-30-174-3
As a shared variation of inflorescence, foliation and leaf
forms with their venation appears
- radial divergence from the same node,
- branching in pairs from a shared node,
- displaced nodes
as steps towards increasing one-way direction from manifold to 2-fold
to 1 single branching.
The displacement of nodes could be suspected as
expression for time: more and more debranched degrees in a dimension
chain transformed to motions, equivalent Time.
Inflorescences, e.g.... umbel.........- 2-sided cyme.......- raceme
Foliation:...................rosette........- opposite..............- alternate (spiralled)
Venation:..................pulmate......- feather type, 1,....- 2, with displaced nodes
Inflorescence:
A sketch on how to regard the variations of inflorescence
in a dimension chain:
In d-degree steps:
5→ 4: Multistage flowers as cymes
imply branching of the main axis, here regarded as representing
d-degree 4. The repeated "center - anticenter" branching shows on
a high potential on this deeper level. These flowers seem all (?)
to have top flowers, eventually an expression for the definition
of new nodes as new centers.
4→ 3: Top flower versus only lateral
flowers may be interpreted as a step from step 4 →
3 in terms of coordinate axes. Branching of these flowers of umbel
type from one node becomes an expression for the radial pole 3b
in our model.
3→ 2: Displaced nodes in raceme
type can express the added motional moment in d-degree 2, from 2-dimensional
rotation to 3-dimensional spiraled motion in d-degree 2 according
to the model: a new factor of Time. The same differentiation appears
within sessile flowers in a step from spadix or composite
to spikes.
3→ 2→
1: The differentiation from multi sided to 2-sided to 1-sided spread
in space becomes an additional differentiation , so among cymes
but also among sessiles from spadix to composite,
2- to 1-sided: the latter connected with step 4→
3: vertical to horizontal axis.
Foliation:
Regarding foliation, the variations radial, opposite and
spread foliation could also be described in terms of angle steps:
- from 360° in rosette and whirled foliation to
- 180° in opposite foliation
- to smaller angles, e. g. 144° or 120°
in spiraled foliation with displaced nodes.
It’s said that most dicots have opposite to spiraled foliation,
while monocots mostly have spiraled ones. Hence, also in this feature
the monocots show a certain displacement towards lower d-degrees
according to first interpretations above.
Such a displacement separate also rosette
from whirled foliation. Cf. radial vector field outwards
in d-degree 4 and radial structure, pole 3b in d-degree 3 in the
model: a rosette at the base of the main axes or stalk, at the origin
in the seed, and the whirled leaves further out.
Leaf forms and venation:
Even in the venation of leaves the stepwise displacement
of nodes are found, from
- a node in the center of shield-shaped leaves to
- radial nerves from edge of the leaf (kidney-shaped or the like)
to
- nerves branched in pairs to
- displaced branching of the nerves (feather veined) to
- parallel veins,
approximately as geometrical steps in d-degrees 4 →
3 → 2 →
1. Parallel nerves become especially common among monocots.
Forms of the leaves follow roughly the venation:
round to oval to linear shape with all variations between.
Leaves with lobes seems to have an animal parallel
in tissue death, for instance in the death of web between toes and
fingers; assumably an effect of the inhibiting gradient from the
00-pole as polarizing force; a polarization of charge?
Some notes about trees:
- It seems as if trees often branch in about 5 steps from root
– trunk out to the leaves?
(This regards Swedish broadleaf trees and is no scientific information.)
Fig Pl-32-165-1
The branching gets often a character of angle steps, one hypothetical
aspect on d-degree steps in the dimension model. (In the schematic
right figure above as → 180°
→ 90° →
45° → 22, 5°
→ 11,25°.)
And the leaves return to earth, i.e. in the inward
direction, with an "energy gap" in the angle rest, ~ the defoliation.
- A developed broadleaf tree gets the form of a magnetic field
around a staff: in at South Pole, out at North Pole.
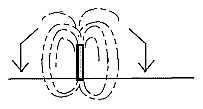 Fig
Pl-33-165-2 Fig
Pl-33-165-2
- Nuclei of branches, born within the trunk, are often groups
of 2 –3 – 4 – 5 in number, so it’s said, and migrate outwards the
bark. (Perhaps a model of how the planet system was born?)
- Like surface of the Earth a tree has negative charge at the surface
and positive in its center, like the atom and in opposition to its
origin , the individual cell. Horizontal parts of plants become
negative charged on the upper side, positive underneath. Hence,
positive charge from inward direction, negative from outward direction,
as in the atom.
(A hazel bush as a cascade particle?)
|

 Fig
Pl-2 (after picture from reference Ps, p. 78)
Fig
Pl-2 (after picture from reference Ps, p. 78) Fig
Pl-3
Fig
Pl-3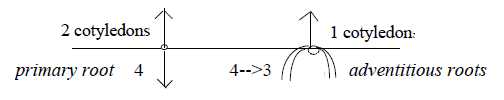
 Fig
Pl-5-166-1
Fig
Pl-5-166-1 Fig
Pl-6-164-1
Fig
Pl-6-164-1 Fig Pl-7-164-2
Fig Pl-7-164-2
 Fig
Pl-8-166-2
Fig
Pl-8-166-2 Fig
Pl-9-167-1
Fig
Pl-9-167-1 Cross section: Fig Pl-10-168
Cross section: Fig Pl-10-168 Fig
11 from reference Sb
Fig
11 from reference Sb Fig
Pl-13-169-2
Fig
Pl-13-169-2 Fig
Pl-14-172-3
Fig
Pl-14-172-3

 Fig
Pl-17-173-2
Fig
Pl-17-173-2 Fig
Pl-18-173-1
Fig
Pl-18-173-1
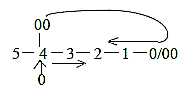 Fig
Pl-20-005-1
Fig
Pl-20-005-1 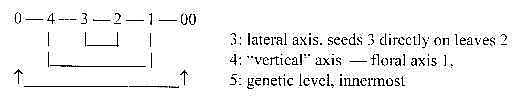 Fig
Pl-21
Fig
Pl-21 Fig
Pl-22-173-3
Fig
Pl-22-173-3

 Fig
P-25-171-1, A seed of conifers with integument
Fig
P-25-171-1, A seed of conifers with integument Fig
Pl-26
Fig
Pl-26 Fig
Pl-27
Fig
Pl-27
 Fig
Pl-29-174-2
Fig
Pl-29-174-2
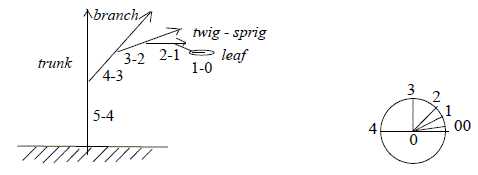
 Fig
Pl-33-165-2
Fig
Pl-33-165-2