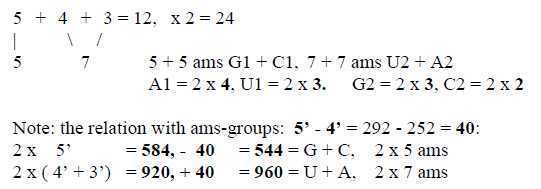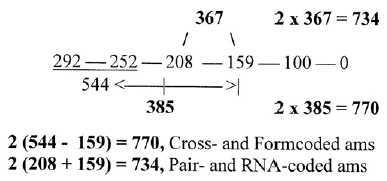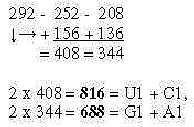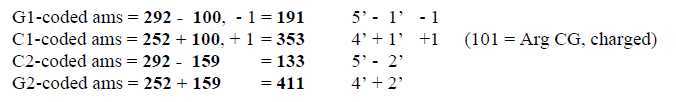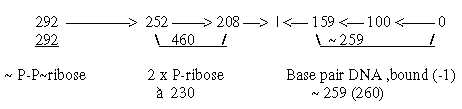ES-chain and main codon domains of ams:
The elementary number series 5 to 0 with exponent 2/3
times 102 shows up to highly correlate with mass distribution on codon domains of ams,
both the division on codons G+C — U+A (544 and 960), the
12-grouos of ams from tables 2 and 3 (770 and 734), codon type
pairs as G+A — C+U and individual codon groups, especially
the G- and C-groups.
1. Total mass and codon groups G+C and U+A:
The series 52/3 - 42/3 - 32/3
- 22/3 - 12/3 - 0, times 100, gives the
abbreviated numbers 292 - 252 - 208 - 159 - 100 - 0. Marking these
numbers 5' - 4' etc. we have that 2 times 5' + 4' + 3' give mass
sum of the 24 ams R = 2 x 752.
Note the correlation with number of ams, 2 x
(5 + 4 + 3).
Fig 3-1: The ES-chain:

To repeat the way of writing:
G1, C2, etc. refer to mass sums of side-chains (R) of ams coded
by G as 1st base and those coded by C as 2nd base respectively
etc.
G+C or U+A refers to the sums of coded ams (R),
equal in 1st and 2nd base order.
G + C = 292 + 252 = 544
U + A = 292 + 252 + 2 x 208.= 960
2. Number of ams, correlating with the elementary
numbers 5 - 4 - 3:
Fig 3-2: Number of ams:
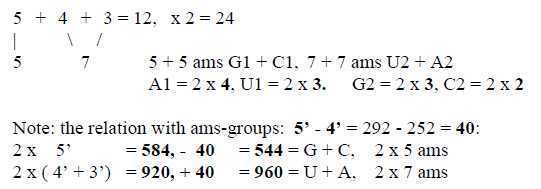
The individual and pairs of codon groups are given through minus/plus
lower numbers or intervals in the series, reminding of the principle
view of debranched degrees meeting "the other way around"
in the background model:
Fig 3-3: A dimension chain, the loop version of the model:
(For a very short description of the model, see here.)
3. Mixed and
not-mixed codons, 12-groups
770 and 734:
The two 12-groups of ams presented in tables
2 and 3 are given directly in a simple way, groups 544
and 208, -/+ 159 times 2:
Fig 3-4: The two 12-groups 770 and 734:
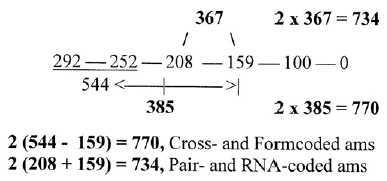
U- and A-groups in 734-group = 2
x 208 + 159 = 575,
G- and C-groups in 734-group = 159
(575 also = 3' + 2' + 1' = 467, + interval 3'
- 1' = 108. UU + AU + AA = 467 +1, Tyr UA = 108 -1.)
GG + GC + CC (Gly + Ala + Pro) = interval 59,
-1,
CG (Arg) = end interval 100, +1.
Arg can transform to Pro leaving its end-group CN3H5 =
59.
[In the background model the last step 1→
0 is interpreted as a step from d-degree 1 into motions. It
has been told that Arginine is especially rich in the tails
of sperms. However, number 101 appears also in other contexts.]
See further details in file The
two 12-groups of ams.
It may be added already here (see further file Mass
division on atom kinds...)
Mass of C-atoms in 770-group = 444 = 544 - 100
Mass of C-atoms in 734-group = 516 = 416 + 100,
Cross- + RNA-codons: ams = 418 + 412 = 830 = 2 x
416, -2
Form- + Pair-codons: ams = 352 + 322 = 674 = 2(544
- 208), +2
Adding bound B-chains to these codon type groups, we
get sums approximately equivalent (~) with the division
in R- and B-chains:
Cross RNA Form
Pair
418 412
352 322 R
+ 336 336
336 336 B
754 748
688 658
= 1502
1346
~ R -2
~ B +2
[In the sum of cross- plus pair-coded ams with R = 740, the close
to equal division between U+G-codons and C+A-codons (the keto-/amino
polarity) should be noted::
UU + GG + UG + GU = 370 -1
CC + AA + CA + AC = 370 + 1
See Short files, 17.9, 3.
370 equivalent with 5 B-chins unbound à 74 A.
370 = 367 +3, the other 2 codon-groups 2 x 382 = 2 x 385 - 3 ]
4. Purine - pyrimidine base pair groups, G+A and C+U:
Base pair group divided in purine and pyrimidine kinds
are shown below. It should be noted that we can regard the whole
chain included through number 934 as 2 x 467:
Fig 3-5: Base pair groups C+U, G + A:

A division of 5', number 544, gives the purine and pyrimidine
codon pairs from G+C, U+A:
Or: G1 + A1 = 960 - 272 =
688
C1 + U1 = 544 + 272
= 816
Halving of 3', number 208, distributed inwards -
"backwards" to 292 and 252 gives both a division
on
codon groups and on atom kinds, see file 04.
4b. Parents of he codon bases with mass 292 distributed to
following numbers:
Number 292 (52/3 x 102) is the sum
of Orotate (156) and Hypoxanthine (136), the parents
to the pyrimidine and purine bases U, C and G, A. Just a coincidence?
Transferred to following two numbers in the
ES-chain, times 2, happen to give the codon domain sums of ams
in 1st base order, curiously enough:
Fig 3-6:
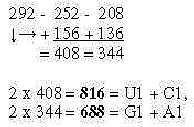
Remains to explain how this rather remarkable, simple derivations
of mass numbers could be interpreted in terms of biological processes.
4c. Keto-/amino-acid polarity, a note:
G1 + U2 = 628 = 920 (2 x 460) - 292
C1 + A2 = 876 = 584 (2 x 292) + 292
5.
Single code base groups:
G- and C-groups illustrate remarkably a similar
-/+ operation of lower numbers in the chain:
Fig 3-7: G-C-groups and numbers 100 -
159:
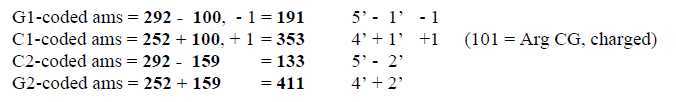
G1 = 292 - 101 = 191, C21
= 292 - 159 = 133
C1 = 252 + 101 = 353. G21
= 252 + 159 = 411
U22 = 544 - 107
= 437 U1 = 252 + 208,
+3
A22 = 416 + 107 = 523 A1
= 208 + 292, -3
1 Note the changed order
from 1st to 2nd base.
U1 and A1 groups are less clear in derivations from the
ES-chain than the G-C-groups;
an alternative view with "polarization" of 544 in +/-
272:
U1 = G1 (191)
+ 272 = 463
A1 = C1 (353) + 416 - 272 = 497
Or:
U2 = 544 – 208 = 336, + 101
A2 = 416 + 208 = 624, - 101
Or:
A1: 500 (= 292 + 208) + ½ x 208 = 604, - 107 (~Tyr) = 497
U1: 460 (= 252 + 208), - ½ x 208 = 356, +107 (~Tyr) = 463
U1 and A1 mass sums of ams may naturally be indirectly derived
exactly though operations from G1+A-group 688, - G1, U1+C1-group
816, - C1.
See also file 04, point 2.
Another way to write the derivations:
G1 = 5' - 1', -1
A1 = (5' + 4') - (3' - 2'), +2 = 497
C1 = 4' + 1', +1 U1 = ( 2 x 3')
+ (3' - 2'), - 2 = 463
C2 = 5' - 2'
U2 = (5' + 4') - (3' - 1'), +1 = 437
G2 = 4' + 2'
A2 = ( 2 x 3') + (3' - 1'), -1 = 523
About Tyr 107 and Arg 101: Since Tyr derives from
Phe, UU-coded, we could eventually regard Tyr as an expression
for the step U2 →.A2. Arg, which gets its end-group from
the G-base, eventually from an G1-code?)
In the same way A1 = 544 - 47, U1 = 416 + 47:
47 = mass of Cys R with UG-codon, as if from Meth AUG-codon -
but Cys generally is regarded as derived from Ser.
With interval 3' - 1' -1 = 107 and 2' - 1' =
59 +1 (see below), the difference become 47.
(In the background model last step 1 to 0 represent
the step to the d-degree of motions. Cf. that Arginine is said
to be especially rich in the tails of sperms! However, number
101 appears also in other contexts.)
(C1 = 4' + 3' = 460, - inerval 3' to 1', +1 ~ Tyr
107.)
Interval 59 in step 2 →1, -/+ 1 = 58 and 60, gives the
difference between code-base groups in 1st and 2nd base order:
C2 = G1 - 58
G2 = C1 + 58
U1 = A2 - 60
A1 = U2 + 60
(Interval 59 in step 2' —1' may be associated with main
contributions from outside into the citrate cycle: acetyl(-Coa)
+ OH, 59 (60) in the step from oxaloacetate 132 to citrate 192.
Corresponding step 4'→> 3' in the ES-chain = 44 ~ CO2,
the preceding contribution in the cycle, with pyruvate giving
malate.
252 ---|---208 -- 159 --|-- 100
44 <— 15 —> 59
COO - CH3 See
more about glycolysis-citrate
cycle.)
Note 1:
Number 544 may be regarded as divided in three ways: 292 -- 252,
336 -- 208 and in interval 544 - 367 = 177 and 367.
C2 = 133 = 177 - 44 (the 2nd interval 4' - 3',
G2 = 411 = 367 + 44
All four 2nd base groups (-/+1) from the interval 44:
544 - 367, - 44 = 133 = C2-coded ams
208 + 159, + 44 = 411 = G2-coded ams
272 + 208, - 44 = 436 = U2-coded ams - 1
272 + 208, + 44 = 524 = A2-coded ams +1
For groups G2 and C2 we have also:
4' + 3' = 460, - middle interval 49 = 411
5''- 3' = 84, + middle interval 49 = 133
Note 2: -/+ Tyr from C1 to U1 ?
C1 = 252 + 208 (= 460), - 107 (~Tyr) = 353.
U1 = 252 + ½ x 208 + !07 (~Tyr) = 463
Note 3: G1-group 191 divided after 2nd base:
GG + GA = 133 = 5' - 2'; GU + GC = 58 = 2' -
1', -1.
Divisions within single base groups in 2nd base order:
In G2 + C2:
1st base G or A: sum of ams = 193, ~ G1 +2 (GG +
AG = 133; GC + AC = 60.).
1st base U or C: sum of ams = 351, ~ C1 - 2 (CG
+ UG = 278; CC + UC = 73)
In U2 + A2:
1st base G2 or A2: sum of ams = 495, ~ A1 + 2. (GU + AU
= 232; GA + AA = 263.)
1st base C2 or U2: sum of ams = 465, ~ U1 + 2 (CU + CA
= 210; UU + UA = 255.)
Number of ams in single base groups with odd number of ams::
Odd numbers of ams Even numbers of ams
G1, 5 ams 2nd base G, A: 3 ams, 2nd base C,
U: 2 ams.
C1: 5 ams. 2nd base G, A: 3 ams, 2nd base C,
U: 2 ams... division 3 -/2
U2: 7 ams: 1st base G, A: 4 ams, 1st base C,
U: 3 ams
A2: 7 ams: 1st base G, A: 4 ams, 1st base C,
U: 3 ams... division 4 - 3.
(Thanks to Tyr without partner)
Two sets of the single base groups in 1st and
2nd base order:
5' 2 x 292 = 584,
- 100 = 484 = C1 + C2 - 2
4' 2 x 252 = 504
+100 = 604 = G1 + G2 + 2
3' 2 x 208 = 416 + 584
- 100 = 900 = U1 + U2 (U1+U2 from the C-groups)
3' 2 x 208 = 416 + 504
+100 = 1020 = A1 + A2 (A1+A2 from the G-groups)
7. Individual codons and amino acid mass numbers:
See file 05.
6. 3rd base groups:
Number 292 as the sum of Hypoxanthine and Orotate, the parents
to the code-bases from which these bases get synthesized, are
connected with differentiation of codons in 3rd base: A/G (+A
or G) or U/C, implying a connection too with 1st base in the anti-codons
in tRNAs.
Mass sum of ams with differentiated codons in
3rd base = 1169 = 4 x 292 +1. It shows up to be divided nearly
equal. (Also a coincidence!?)
G1 + A1: 584
= 2 x 292
C1 + U1: 584 +1. = 2 x 292
+1
All ams with indifferent 3rd base = 335 = 544 - 208 = 336,
-1
(336 if Pro CC before ring closed.)
ES-chain with intervals in steps 5' - 4' - 3':
292 --- (40) --- 252 --(44) -- 208
4 x 292 +1 = sum of ams with differentiating
3rds base in codons.
4 x 40 = 160, -
1 = 159 = "2-base-coded" ams among non-mixed codon
group
4 x 44 = 176
= "2-base-coded" ams in the group with mixed-codons.
4 x 208 = 832 = G2 + A2 with
differencing 3rd base:
G2: 1 x 208 + 101, A2: 3 x 208 - 101.
4 x 84 = 336, +1 = C2 + U2
C2: 0 + U2: 337
We get 8 ams in each group
8 ams with 3rd base A/G or A or G = 638 (3 ams only one
choice: AUG, AUA, UGG),
8 ams with 3rd base U/C =
531
8 ams with indifferent 3rd base =
335
Numbers 638 and 531 may eventually be derived in this way:
A/G-coded ams: 272 + 367 = 639,- 1 = (½
x 5' + 3' + 2') -1
U/C-coded ams: 272 + 259 = 531
= (½ x 5' + 2' + 1')
8. Some extra annotations to base pair groups:
a) 84 = interval 292 - 208 = 5' - 3'
U+A: 960, - 84 = 876 = C1
+ A2
G+C: 544, + 84 = 628 = G1 + U2. (C1 + 84 = U2)
C2 + U2 = 570, + 84 = 654 = G1 + U1 = C2 + A2
- 2
G2 + A2 = 934, - 84 = 850 = C1 + A1 = G2
+ U2 +2
In general terms these number operations as +/-
84 (5' ↔ 3') could express a process outwards - inwards:
“5 → 4 → 3 → ← 3← 4 ←
5”.
b) Examples of similarities in N and Z between base pair
groups:
N-number: G1 + U1 = 299
= 299 = A2 + C2
G2 + U2 = 377 = 377
= A1 + C1
Z-number: G1 + U1 = 355
+2 = 357 = A2 + C2
G2 + U2 = 471 +2 = 473 = A1 + C1
Crosswise addition N-Z between G2-C2-groups, U2-A2-groups gives
the same numbers as Cross- plus Form-coded ams = 770, RNA- plus
Pair-coded ams = 734:
G2: N + C2: Z = 262, → 734 ← 472 = U2: N +
A2: Z. Interval 208 +2.
G2: Z + C2: N = 282. → 770 ← 488 = U2: Z +
A2: N. Interval 208 - 2.
c) Displacements 220 and 26 between groups in
1st and 2nd position:
G1 to G2 and C1 to C2: +/- 220 = 2 x 110 and A1 to A2: -/+ 26
(See further file 7 and file 13 about N-Z-division.) U1
to U2
It may be noted here that
G+C = 544, + 26 = 570 = C2 + U2,
(G2
411 + 26 = U2 437. C2 133 + 26 ~ 159, - 26 = 107.)
U+A = 960, - 26 = 934 = A2 + G2.
U+A = 960, - 110 = 850 = C1 + A1 (~ U --> C);
960 - 220 = 740 = Cross + Pair coded ams
G+C = 544, + 110 = 654 = G1 + U1 (~ C --> U); 544 +
220 = 764 = Form + RNA-coded ams.
9. Some general
annotations:
a) Half the number 292 = 146 is the mass of α-ketoglutarate,
from which Glu (147 A) derives directly with a central role for
amination of the amino acids
b) 146* happens also to be the number of base-pairs in
DNA winded around the histones in chromosomes. Why this
curiously exact number? *(Later in Wikipedia changed to 147.)
c) 292 is also the mass of P-P-ribose part of bases
in the form of coenzymes.
(Ribose 150 + two H3PO4
(98, x 2), - 3 x H2O).
d) Another feature is that G- and C-coded ams "come
first" in the ES-chain as connected with the numbers 5'-
4'. This agrees with what scientist have found in experiments
where ams appear in liquids. There are also indications of a pressure
towards more A-T-rich DNA during evolution according to the scientists,
as in agreement with steps 5' → 4' →3' in the ES-chain,
ams with A-U-codons including number 2 x 3'.
e) P-ribose groups in nucleotides:
e1) The P-ribose-groups in chain binding = 195 uncharged,
194 charged (64 or 63 + 131):
584, 2 x 292 in the ES-chain → 3 x 195 (-1).
Could this number from the ES-chain perhaps be one aspect on
the cause for triplets of the bases in codons?
e2) A suggestion by Copley et al (2005) is that ams could
have been synthesized at the inner OH-group of ribose in a string
of nucleotides. In the illustration to this hypothesis a P-P-¨ribose
group binds to two nucleotides.(P-ribose + bases). The whole ES-chain
could somehow illustrate the mass numbers where the synthesis
of ams should appear in the middle step :
Fig. 3-8: Copley-figure numbers in
ES:
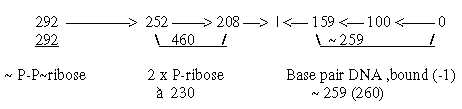
(P-P-ribose: 2 x 98 + 150, - 3 x 18 =292, P-ribose: 98 + 150,
- 18)
Yet, here is counted with ribose in RNA, not
deoxyribose, but with base pairs in DNA with the T-base instead
of the U-base. Bonds (-18) to the bases also neglected or somehow
occurring in the middle step. (Cf. 385 - 367 = 18. 544 - 159,
208 + 159).
A little extra note about log-numbers 52,
42, 32:
lg 25 / lg 3 = 2.929947
lg 16 / lg 3 = 2.523719...Sum 5.453666
lg 9 / lg 3 = 2.0
Testing of the ES-chain?
1) Only e.g. heavy water or other deviating isotope of C, N or
O in the type of Miller experiment. Does it
change the reactions in any way?
2) Construct a peptide with atomic masses in accordance with the
ES-chain, e. g .:
Glu,Glu,Lys,Glu - His,Gln,Leu,Pro - Trp,Cys,Ser
- Ala,Gly,Pro - Arg ?
(In a liquid of Miller type, with small variations in pH. Does
it have any effect?
A Survey of derivations of codon-grouped ams sums from
number in the ES-chain is available
here.
To Mass distribution
on other bases than codons