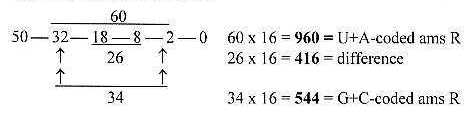The investigation started in the 1980th - without prejudices -
with a table of 20 + 4 codons (Table I) with and A-, N- and Z-numbers
of side-chains (R) of the coded amino acids (ams), 4 ams having
two different codons. Most common isotopes were used.
Hence, codons where the choice of purine bases
U and C in 3rd position or of pyrimidine bases A and G in 3rd
position makes no difference was counted as one and the same,
as when 3rd base makes no difference at all (called "2-base-coded",
generally in the literature called "degenerated"). The
4 ams with double codons are Arg CG + AG-A/G, Ser UC + AG-U/C,
Leu CU + UU-A/G and Ileu AU-U/C + AUA, only differing in 3rd base
type.
In these files all numbers will refer to atomic mass (nucleon
number) and to side-chains (R) of ams where nothing else is mentioned.
Table 1: Codons and A-, N, Z-numbers in side chains
of 20 + 4 amino acids:
|
1st base
|
2nd base
|
Ams
|
N
|
Z
|
A
|
..........
|
A
|
Z
|
N
|
Ams
|
1st base
|
2nd base
|
|
G1
|
G
|
Gly
|
-
|
1
|
1
|
|
1
|
1
|
-
|
Gly
|
G
|
G2
|
|
|
C
|
Ala
|
6
|
9
|
15
|
|
101
|
56
|
45
|
Arg1
|
C
|
|
|
|
U
|
Val
|
18
|
25
|
43
|
|
130
|
69
|
61
|
Trp
|
U
|
|
|
|
A
|
Asp
|
28
|
31
|
59
|
|
47
|
25
|
22
|
Cys
|
U
|
|
|
|
A
|
Glu
|
34
|
39
|
73
|
|
31
|
17
|
14
|
Ser2
|
A
|
|
|
|
|
|
|
|
|
|
101
|
56
|
45
|
Arg2
|
A
|
|
|
Sum
|
5
|
|
86
|
105
|
191
|
|
411
|
224
|
187
|
|
6
|
Sum
|
|
C1
|
G
|
Arg1
|
45
|
56
|
101
|
|
15
|
9
|
6
|
Ala
|
G
|
C2
|
|
|
C
|
Pro
|
18
|
24
|
42
|
|
42
|
24
|
18
|
Pro
|
C
|
|
|
|
U
|
Leu1
|
24
|
33
|
57
|
|
31
|
17
|
14
|
Ser1
|
U
|
|
|
|
A
|
Gln
|
33
|
39
|
72
|
|
45
|
25
|
20
|
Thr
|
A
|
|
|
|
A
|
His
|
38
|
43
|
81
|
|
|
|
|
|
|
|
|
Sum
|
5
|
|
158
|
195
|
353
|
|
133
|
75
|
58
|
|
4
|
|
|
G1+C1
|
10
|
|
244
|
300
|
544
|
|
544
|
299
|
245
|
|
10
|
G2+C2
|
|
U1
|
G
|
Cys
|
22
|
25
|
47
|
|
43
|
25
|
18
|
Val
|
G
|
U2
|
|
|
G
|
Trp
|
61
|
69
|
130
|
|
57
|
33
|
24
|
Leu1
|
C
|
|
|
|
C
|
Ser1
|
14
|
17
|
31
|
|
57
|
33
|
24
|
Leu2
|
U
|
|
|
|
U
|
Leu2
|
24
|
33
|
57
|
|
91
|
49
|
42
|
Phe
|
U
|
|
|
|
U
|
Phe
|
42
|
49
|
91
|
|
57
|
33
|
24
|
Ile1
|
A
|
|
|
|
A
|
Tyr
|
50
|
57
|
107
|
|
57
|
33
|
24
|
Ile2*
|
A*
|
|
|
|
|
|
|
|
|
|
75
|
41
|
34
|
Meth
|
A
|
|
|
Sum
|
6
|
|
213
|
250
|
463
|
|
437
|
247
|
190
|
|
7
|
|
|
A1
|
G
|
Ser2
|
14
|
!7
|
31
|
|
59
|
31
|
28
|
Asp
|
G
|
A2
|
|
|
G
|
Arg2
|
45
|
56
|
101
|
|
73
|
39
|
34
|
Glu
|
G
|
|
|
|
C
|
Thr
|
20
|
25
|
45
|
|
72
|
39
|
33
|
Gln
|
C
|
|
|
|
U
|
Ile1
|
24
|
33
|
57
|
|
81
|
43
|
38
|
His
|
C
|
|
|
|
U
|
Ile2*
|
24
|
33
|
57
|
|
107
|
57
|
50
|
Tyr
|
U
|
|
|
|
U
|
Meth
|
34
|
41
|
75
|
|
58
|
31
|
27
|
Asn
|
A
|
|
|
|
A
|
Asn
|
27
|
31
|
58
|
|
73
|
42
|
31
|
Lys
|
A
|
|
|
|
A
|
Lys
|
31
|
42
|
73
|
|
|
|
|
|
|
|
|
Sum
|
8
|
|
219
|
278
|
497
|
|
523
|
282
|
241
|
|
7
|
|
| U1+A1 |
14 |
|
432 |
528 |
960 |
|
960 |
529 |
431 |
|
14 |
U2+A2 |
*Ile, AU-codon, only differing in type of 3rd base.
(Other tables on different pairing of
codon groups of ams, atom kinds and atomic numbers are give here
in word.)
First observations:
First to notice is that the mass sums of the two main groups with
G+C-codons and U+A-codons become the same in 1st and 2nd base order,
544 and 960.
It implies that mass sums of ams with mixed codons
changing position between the groups are the same, 385 (Table
2). These groups showed astonishing regularities, which seemed to
support the hypothesis that mass distribution of ams on different
codons wasn't a random one. Note the approximately equal sums horizontally
and vertically, Table 2:
Table 2: Mixed codons 12 amino acids, sum 385:
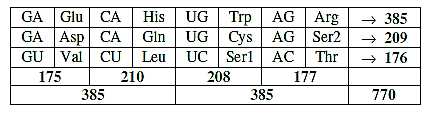
The table is closer studied in file The
two 12-groups of ams.
It led to a division of the 24 codons in 2 main groups of 12 ams,
the other = 2 times 367, (Table 3), which doesn't show the
same regularity as the other:
Table 3: Non-mixed
codons. 12 amino acids, sum 734:
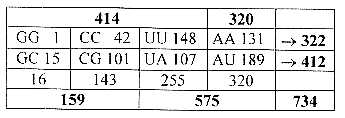
This way of counting and organizing codons seems deviating from
most other research.
We get 4 subgroups of codons, here called Form-, Cross-, Pair- and
RNA-codons:
Form-coded: GA, AG, UC, CU, 6 ams, sum 352
Cross-coded: GU, UG, CA, AC, 6 ams, sum 418...2 x 385 = 770
These two in Table 2.
Pair-coded: GG, CC, UU, AA, 6 ams, sum 322
RNA-coded: GC, CG, UA, AU, 6 ams, sum 412...2 x 367 = 734
These two in Table 4.
Note in Table 3:
G1 + A1, 175 + 177 = 352, give the same mass as the Form-coded
ams,
U1 + C1, 208 + 210 = 418, give the same mass as the Cross-coded
ams.
Before going on with the analysis, two annotations:
Survey of totals:
With mass in unbound backbone chains (B, B-chains) à 74 A,
- 1 in the four ams Arg1 and 2, Lys and Pro. and mass 56 in bound
ams, this gives following survey of totals:
24 ams: R: 1504, B unbound 1772, sum 3276
A,
24 ams: R: 1504, B bound 1344, sum 2848 A.
N-Z: R: 828 Z, 676 N, R+B: 1516 N, 1760
Z, unbound ams.
Cf. for instance codon domains when we count on two sets of ams
R+B, 1st plus 2nd base order, file
17 short files, 2.6.
Simple variations of the elementary number chain 5-4-3-2-1-0:
There are some simple variations of the elementary number chain
(5-4-3-2-1-0), closer dealt with in files in section II, files 12-16,
that more or less approximately give the division between some main
codon groups of ams, G+C and U+A, but also other more detailed ones.
Hypothetically such simpler chains on integers
5→0 with exponents 4, 1, 3, 2 could underlie the more developed
and differentiated chain in this section, precede this in a perhaps
"inflationary" evolution of the code or represent underlying
levels? Here only a couple of examples:
Reading the simple chain as triplets 543+432+321+210
gives 543 (G-C-group -1, U-A-group 960 +3,
Fig 2-1: The triplet series 543 - 432 etc.
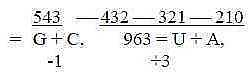 Sum
1506 = total of 20 + 4 ams R, +2. Sum
1506 = total of 20 + 4 ams R, +2.
With exponent 4 the main division 544 - 960 (+2) derives
from first three numbers 54-44-34
plus/minus 3rd number 81: G-C-group 544 = 625 - 81, U-A-group
960 (+2) = 625 + 256 + 81.
With exponent 2 in the 2x2-chain behind the
periodic system, times a factor 16, several different codon-groups
of ams appear (+/-1), the main division showed in figure. 2-2:
Fig. 2-2: Relations to 2x2-series, 34-26-60
times a factor 16:
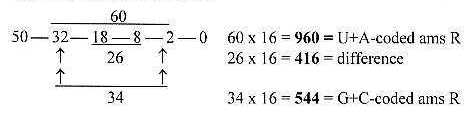
Total sum of the chain, 110, times 16 = 1760, the total Z of the
24 ams (R+B).
See further file Simpler
number chains about the 2x2-chain.
To The exponent
2/3 series (ES)
|


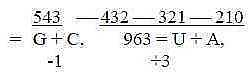 Sum
1506 = total of 20 + 4 ams R, +2.
Sum
1506 = total of 20 + 4 ams R, +2.