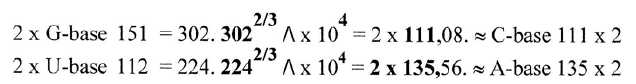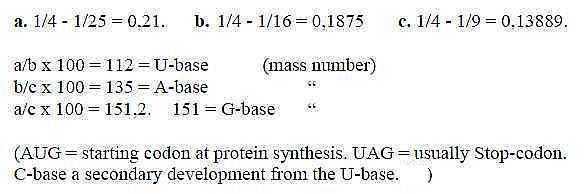Codon bases G, C, U, A in RNA; T instead of U in DNA:
Some material from file Biochemistry 04:

1. Complementarities and inversions:
At least in actual cells of today the bases are synthesized in complementary ways: the purine type from the amino acid Gly as centre, the pyrimidine type from the amino acid 
Asp together with carbamoyl phosphate.
   In both cases circa molecules of circa 60 A are added: Gly 75 + 60 = A-base 135, Asp 133 + carbamyl ~ 60 A to Asp 133 (- 2 x 18 at condensation to Orotate); cf. interval 159 - 100 in the ES-chain.  
   Both mass numbers of Gly and Asp are found in the ES-chain as intervals:

Gly 75 A = 292 - 367
Asp 133 A = 292 - 159...Sum 208 = 3'

It could also be observed that these numbers are inversions of each other:

75 /\ 133... x 10x, = 3/4 - 4/3 x 100

Approximate inversions are also the mass sums of purine versus pyrimidine bases:

G 151+ A 135 = 286. U 112 + C 111 + T 126 = 349:

286 /\ 349.65 x 10-5

2. Exponent 2/3:
Pairs of the RNA-bases - with exponent 2/3 appear to be inversions of their complementary ones:

Fig 10-1: Pairs of bases as each other's inversions through exponent 2/3: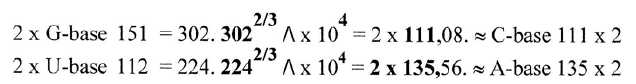

Another relation to the ES-chain:
The single bases as bound (= -1) with exponent 2/3, (figure 10-2 below), times 10, give the sums G + A≈544, U + C ≈ 460, sums 5'+4' and 4+3´ in the ES-chain. With exponent 2/3 applied again on the four obtained numbers the sum becomes ≈ 159 = 2' in the ES-chain. First obtained four numbers without times 10 are ≈100 = 1'.

Fig 10-2: Bases bound with exponent 2/3:

      
3. ES-numbers, a few first notes:

Parents of the bases (hypoxanthine 136 and orotate 156 ) = 292 = 5'

N-Z-division in 4 DNA-bases:
4 DNA-bases, sum 523 A: N-Z compared with numbers in the ES-chain:

Z:  272 = 544 x½. G + C: 136, A + T 136 (- 8 in RNA with U-base = 128)
N: 251 = 252, -1: G + C: 126, A + T 125 (- 6 in RNA = 119)

Mean value of a base pair of DNA:
Mean value of a base pair of DNA happens to be a quotient from the ES-series:

544 / 208, x 100 = 261,5.

Five bases. including T = 635, circa 292/460  x 10^3 ( 634,7)

A step of polarization outwards can be recognized from G + C-bases to U + A-bases, reminding of order of dominating groups in the ES-chain:
   The bonds G ≡C are 3 versus 2 in U=A-pair and G + C include both N and O in the H-bridges, while these are "polarized" to only N in A-base, only O in U/T-bases.

4. Atoms in the bases - a 2-dimensional table:

Fig. 10-3: Atoms in the bases - a 2-dimensional table

Number of atoms in 24 codons, 1st and 2nd bases:

For  23 ams, without AUA-codon for Ile2, the sums become

   horizontally 401 - 15 = 386, 273 - 12 = 261,
   vertically     401 - 16 = 385, 273 - 11 = 262

(The division of 385 on N and C vertically in 209 - 176, the same as in the table of mixed codons.)

Sum of atoms in 24 ams = 674, 2 x 337 . Assuming an equal distribution of bases in 3rd position we get the sum  1011 = sum of the whole ES- series:

292 - 252 - 208 - 159 - 100 - 0      Sum 1011
    544                 467

Number of atoms in the bases and adding equal number in 3rd base:

13 U with 12 atoms = 156, + 6 x 12 = 228
15 A with 15 atoms = 225, + 6 x 15 = 315...Sum 544 -1
11 G with 16 atoms = 176, + 6 x 16 = 272
  9 C with 13 atoms = 117, + 6 x 13 = 195...Sum 467

The equivalences could be connected with the function that the bases have as coenzymes in relation to the different classes of substances. Roughly:
U-base (UTP) with carbohydrates (with dominating atom O),
C-base (CTP)- with lipids (characterizing atom may be said to be H)
G-base (GTP) with proteins (with typical atom N).
A-base: (ATP), main energy storage and with transporting function ? (C-skeleton?)

5. Bases U, A, G from "phase waves":
   (From index file, figure 01-1..) 
Quotients between wavelengths (n = 2, m = 5, 4, 3) in the Balmer series times 10² happen to give the mass numbers of U- and A-bases too (112 and 135) and approximately the G-base (151,2), which could awake some suspicions...* (Quotients as a kind of phase waves? Alleged not to carry any information!)

Fig. 10-4: From Balmer series for spectral lines of hydrogen:

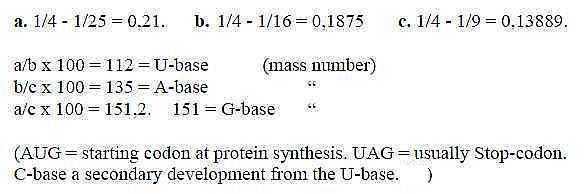
  (C-base eventually later developed to give two pairs? Eventually from a quotient between a spectral line of hydrogen and oxygen.
      (Or cf. last  term in c. = 1/9,  x 1000, = 111,1. C-base = 111 )

---

6. Just some numbers. a selection of operations

a) Sum of 1st and 2nd bases in 24 codons = 6141.
   Quotient to sum of 24 ams R + B unbound 3276:

    6141 / 3276 = 1..8745 ~ 1.875. = 15/8 = 5 x 3 x 1 / 4 x 2, odd/even d-degrees.

    (Cf. 0.1875, 2nd spectral line of hydrogen.

For number 6141 = number 1357 transformed to number base system (nb-x) 6,
see file 19, fig. 19-3.

b) DNA-bases with +2 for double-bonds in the rings:

A = +8, G = +6, C = +4, T = +2 = 543.

c) - 14 (A+T = 261), /\, x 10^7 = 2736.7
    - 10 (G+C = 262), /\, x 10^7 = 3816.8
                        Sum = 6553.5 = 2 x 3276.76. ~ 2 x 24 ams R + B unbound

                       [6 x 509 (24 baser RNA) = 3054, /\, x 10^7 = 3274.4 ]

d) 4 RNA-bases = 509 and number 32

25/2π, x 100 = 509 (509.3)
(4th root of 32x100 ~ 752.12 x10-2, 752 half the sum of 24 ams R)

e) G/5 + A/4 + T/3 + U/2 + C/1 = 273 (272.95),
                                       273 the mean value of two ams R+B unbound

f) 4 DNA-bases = 523 A: 5232 = 2735.29 x102
                                       2735 = sum of 20 amino acids, R+B-chains,
                                       without the extra set of 4 ams with two codons.

g) G-base, mass number from the simple dimension chain:

  1 / 543 + 1 / 210, /\ = 151.43. ~ G-base 151

More material may be found in files about biochemistry:
   The protein synthesis
   Synthesis of the bases
   Numbers: DNA/RNA

*

To Transmitters and the ES-chain.