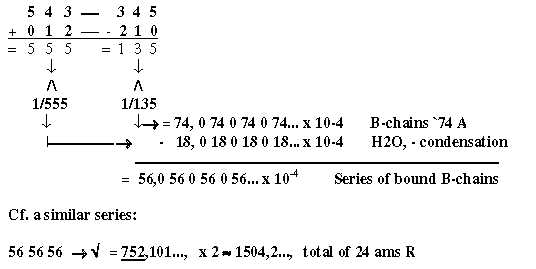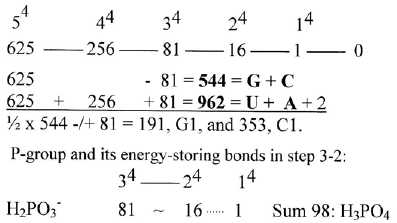I. The triplet series, x1:
a) Reading triplet numbers in the elementary chain 5 - 0:
(Most of this file from "17 short files", 05.)
The most elementary chain 5-4-3-2-1-0 read as triplets approximates
the sum of R-chains of ams read as two triplets: 2(543 + 210) =
1504 +2, or read as 4 triplets as in figure 15-1.
Expanded with triplets from 987 - 876 etc. the chain gives the approximate
whole mass of 24 ams. Intervals in each step = 111 sum up to 24
times B-chains à 74.
Fig 15-1: Triplets
from elementary chain 5 to 0 and the same chain expanded:

A note about number 3282:
Number 3282 is also the difference between products of base pair
numbers:
G 151, C 111, U 112, A 135:
2 x G x C = 33522
|------- 3282
2 z U x A = 30240
3282 = 6 x 547. 5 x 547 = 2735 = 20 ams, without the
double-coded ams.
(½ x 3282 = 1641 is said to have something
to do with a formula for first amount of prime numbers.)
A "condensed" or undeveloped elementary chain 5 - 0, dimensionally, written:
5 - 4 -3 - 2 - 1 - 0, ~ 5433 ~ 546 ("before
disintegration") =2 x 273.
= 3
546 x 6 = 3276, the sum of 24 ams R+B unbound.
b) A-N-Z-numbers of ams approximating the triplets:
Fig 15-2: A-N-Z-
as triplets in codon groups:

The chain A→> N→>Z
implies polarization steps from mass to charge as assumed in the background
model.
Cf. figure 13-8 file 13, approximate the same numbers halved.
[A connection with the ES-chain and its first nummber 5´ ?
1/543 - 1/210 = - 292,03. x 10-5 ]
c) B-chains:
In a peptide bond between ams their side-chains come to point in
opposite directions.
For the triplets 543 and 210 arranged in such a way, see figure
16-2 below,. When read in opposite directions, we get the B-chains
of 12 ams à 74 A = 888 as divided 543 + 345.
Fig 15-3: Triplets
543, 210 written as neighbor R-chains in opposite directions:
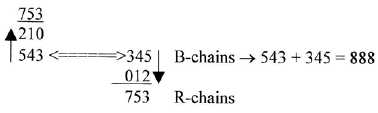
888 = 12 B-chains à 74 A: the division on numbers 543 and 345 gives:
543 / 12 = 45,25 ~ 45 A = COOH
345 / 12 = 28,75 ~ 29 A = H2N-CH
The B-chain gets approximately divided in the COOH-part 45 and H2N-CH-part
29.
Cf. the similar division in the ES-series
here.
345 —|— 210
135 = mass of
the A-base
135 is also mass of Meth, R+B, when losing its end group CH2 =
-14 at start of protein synthesis.
012 + 345 = 357 = sum of A+C+C, the common ends
of tRNA.
Sum of a triplet chain "inwards" 012-123-234-345
= 2 x 357.
A-base 012+123 = 135, plus first two intervals = + 2 C-bases
111 = 357.
B-chains as periodic numbers:
Fig 15-4:
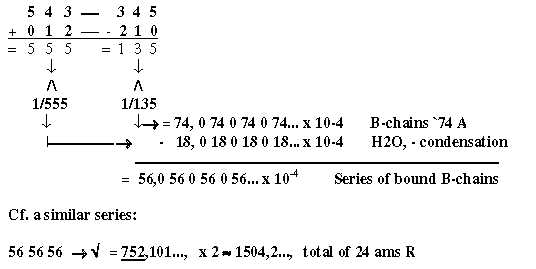
A note:
543/3 = 181 = Tyr, R + B
321/3 = 107 = Tyr R.
Two steps in the triplet series = -222 = 3 x 74, the normal B-chains unbound
Two more numbers from the elementary chain 5 - 0:
4/5 + 3/4 + 2/3 + 1/2 = 1/2 x 5,433333
[1/5 + 1/4 + 1/3]4 = 376,5. x 10-3; x 2 x 103 = 753,037.
About the elementary series as exponents to 2 as
a binary language and Serine, see file 17.18.
II. The x4 series:
The x4 series as an underlying chain?
It would agree with the general thoughts behind this research that
chains as x4 and x3 (x = 5 - 0) could underlie
the ES-chain on deeper levels.
In the chain, figure 15-2 below, we have that 625 - 81 = 544, the
G+C-coded ams and 625 + 256, + 81 = 962, the U+A-coded ams +2. The
operation -/+ 81 in this series x4 is comparable
with the similar operation -/+ 208 in the ES-chain.
Fig 15-5: An
x4-chain, some codon groups of ams:
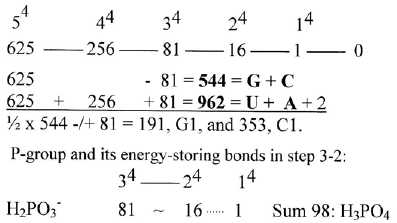
Number 81 is both a charged molecule H2PO3 but also the R-chain
of His (the only ams that not derives from Glycolysis-Citrate cycle
but from the A-base).
It could be observed that -/+ 81 gives the individual
codon base groups in 1st order in the ES-chain:
½ x 544
-/+ 81 = G1 191, C1 353,
544 - 81 = U1 463
416 + 81 = A1 497. (An eventual influence
of phosphorus groups, P-group H2PO3~ = 81 or of His, R 81?)
Sum 44 + 34 = 337 is 1/3 of the total sum
of the ES-chain.
*
To An x3-chain ?