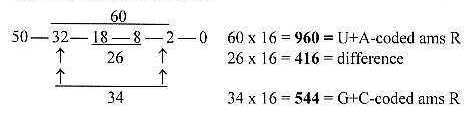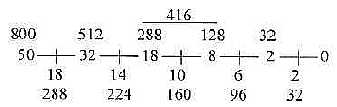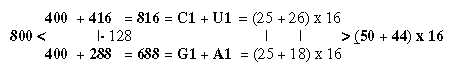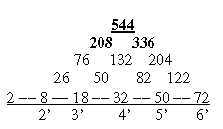However, number 544 appears also "linearly" as a sum:
(32 - 8) x 16 = 384
(18 - 8) x 16 = 160
Sum: 544
It may be noted that first three numbers 50 - 32 - 18 in the 2x2-chain times a factor ~ 30 (2 times the elementary series 5-0) roughly approximate the sum and division on U+A and G+C groups: 1500 - 960 - 540.
3. Some general observations:
Both 208-numbers in the ES-chain and here 416 goes to the
U+A-group of ams. Cf. perhaps that additions 8 and 18 are repeated
two times to whole shells in the periodic system (through displacement
of d-orbitals; s-orbitals of next shell first filled).
262 = 676, the middle number 18 + 8 in this 2x2-chain squared, times 2 = 1352, sum of all ams R without H-atoms; this factor 26 also something to remember. Total number of ams, R + B = 3276 = 26 x 126.
Number 94, 60 + 34; and Selenocysteine:
Number 94 (times 16 = 1504, total of ams R) is also the R-chain
of the so-called 21st ams Selenocysteine, 34 Z, with isotope
79 of Selenium: A (R) = 94 = 2 x 47, the R-chain of Cys with its
special role in protein folding. Se-Cys is encoded in a special
way and could be an example of how Nature elaborates to fill arithmetical
patterns?
About numbers 94, 47, 34 and the division of number 128, see Subpages I, file 04. point. 6
Total number of atoms in R of the 24 ams without H-atoms = 224 = 14 x 16.
(14 the interval in step 4" - 3").
(Cf. facor 43 in
Z-sum of elements (point 6) in f-orbitals for the "stable" 1-83 Z:
1/43 = 2325,5 x 10-5t. 2325 = Z-sum of elemets in d+p-obitals.
Z-sum in s-orbitals (of elements 1-83Z) = 258, 1/10 of the sum of elements in s- + p- + d-orbitals, 2583, like the approximate sum of H-atoms of the total sum in the R-chains of ams R.)
4. All integers 1 - 110 = 6105:
Another curious connection is that the sum of all integers 1 - 110
of the whole chain = 111 x 55 = 6105, inverted = half the total
sum 3276 of 24 unbound ams 1638 as a periodic number,
Fig 13-4: 6105,
total sum of numbers 1-110:

* Numbers 18 and 180 as decimal periods are equivalent
with masses of H2O and glucose, fructose,
essential starts for ams!
5. Mass numbers, other groups:
Fig. 13-5. 16 times the 2x2-chain:
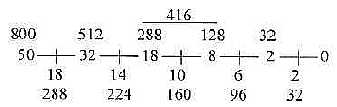
a) The two 12-groups of ams, 770: and 734, -/+2 = 768 and 736:
12-group 770, ams with the mixed codons, -2 = 768, 2 x 384:
384 = 800 - 416 (or 512 - 128 or 416 - 32),
an interval here as in the ES-chain.
384 divided in numbers 208 and 176;
- 208 = 1/2 x 416, = 3' in the ES-chain.
- 176 = 1/2 interval 512 to 160 (128 + 32)
Note the similarity in derivations with the ES-chain: in these groups:
384 is an interval of the type 52/3 —— 22/3 (x10^2) in the ES-chain.,
and the other 12-group (734 + 2) appear in the middle step as in that chain,
both 288-nuumbers belonging to the 734-group.
Cf. numbers in paragraph xx below. Cf. below Pyramid numbers.
b) Purine - Pyrimidine pairs:
Fig. 13-6: Sums of ams R in codon groups:
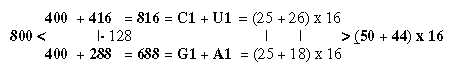
c) B-chains:
B-chains bound = 1344:
Orbital numbers (18 - 14 -10), x 16 = 288 + 224 + 160 = 672, x 2 = 1344
= 6 x 224.
Why a factor 16?
- Cf. the simple chain 5x4, 4x3, 3x2, 2x1, the sums 20-12 - 6 - 2 squared, times
2,
(see 17 short files, 8.2), which gives the numbers 800 and 288, with interval 512 from 4x4..
- Factor 16 happens to appear in all single base groups in 1 1st base order -/+1:
G1: 192 -1, C: 352 +1, U1 464 -1, A1 496 +1.
Why, however, this factor 16 here, if pointing to a real connection
between this 2x2--chain behind the periodic system and codon-grouped mass in the genetic
code?
- As 24, an expression for d-degree 4, four polarizations
inwards?
(16 also the inversion of 54, x 104.)
- And / or the factor biochemically related to mass of oxygen 16O,
4 alpha - or Z of 32S in a first energy source?
- Or somehow connected with the unexplained "octet rule"
with a doubled expression for mass in the atomic nucleus?
It must be left here as an open question.
6. Atomic mass expressed in the levels of electron orbitals and shells?
It is natural that the distances of electron orbitals and intervals between them around an atom are expressions for atomic mass, e.g. number of charged nucleons in the nucleus and thus circa half the atomic mass of ordinary isotopes of C, N, O and S in ams.
1760 was factor 16 times the sum of the 2x2-chain and the total Z of 24 unbound ams R+B, i. e. sum of all electrons.
The number of atoms C, N, O, S in these unbound
ams R+B is 224.
Reducing 1760 with this number 224 in steps -
as a kind of activation in electron shells, as suppressing of deeper
orbital levels, with one electron in each step until those of C-atoms
are zero, gives 6 "phases". It gives
stepwise mass of bound ams R+B and disintegration of R-chains doubled.
Fig 13-7: Reducing
1760 with 224 per step:
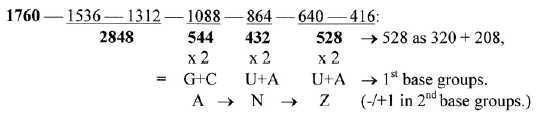
2848 is the mass sum of the 24 bound ams, R+B, here from phases representing suppression of electrons in the K-shell.
- 1536 is the sum of all 128 C-atoms, 1312 sum of
all other atoms.
Whole interval 1760 — 416 = 1344, sum of 24 bound B-chains,
4 x 56 in each step.
544 is also the mass sum of all other atoms N, O, S, H in
R-chains,
960 = 432 + 528, the mass sum of the 80 C-atoms in R-chains.
432 = 36 C-atoms in C2 + U2, 528 = 44 C-atoms in G2 + A2.
Sum of whole chain = 14 x 544.
Classes I and II of tRNA synthetases: I = aa 976 +1, II = aa 528 -1:
1088 + 864 = 2 x 976
640 + 416 = 2 x 528
Series of phases for R- and B-chains taken separately:
R-chains: 104 atoms C, N, O, S gives minus 104 per step. (H = 152)
B-chains:
120 atoms C, N, O gives minus 120 per step. (H = 92)
Z
-sum R-chains 828.
Z-sum B-chains 932.... Difference 104.
B: 932 - 812 - 692 - 572 - 452 - 332 - 212
1504
R: 828 - 724 - 620 - 516 - 412 - 308 - 204
1344
Thus, the B-chains give in first numbers the atomic mass sum of the 24 R-chains,
the R-chains in first numbers the sum of the atomic mass sum of 24 B-chains bound.
7. Z-numbers, the total and its divisions:
Fig 13-8: Division
of total Z 1760 in the 2x2-chain times 16:
The total 1760 divided 800 and 960: 800 = 512 + 288, numbers from 4 and 3.
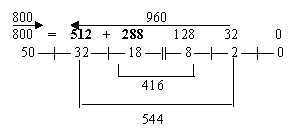
Sum of whole chain = 110, times 16 = 1760 = total Z-sum
of 24 ams (R + B) unbound.
960 = 24 x 40, Z-sum for B-chain of Gly with only 1 H as "R-chain".
Displacements of H-atoms between R- and B-chains:
If in B-chains one H is added as replacement for R-chains, and
the 4 H, reduced in B-chains of Arg 1, 2, Lys and Pro, are filled
from R-chains, all B-chains become NH2-CH2-COOH
= 40 Z: It gives a division of the chain in step 5 - 4:
R-chains: 800 Z = 50 x 16
B-chains: 960 Z = (32 + 18 + 8 + 2) x 16
= 24 x 40 Z
(32 + 18) x 16 = 20 B-chains. The 4 extra B-chains = (8 + 2) x 16.
R-chains, number 800 Z get divided:
A1+U1: 512 = 32 x 16. (528 Z - 14 H - 2H
in Arg AG and Lys AA)
G1+C1: 288 = 18 x 16. (300 Z - 10 H -
2H (in Arg CG and Pro*)
* (Has sooner to be added + H in Pro, compensated
with - 2H in Glu and Asp?)
These resulting numbers 512 and 288 could give more support for a hypothesis that the 2x2-chain
influenced the code on one level and for the thought that the B-chains may have "come first" in the evolution, followed by a stepwise construction of the side chains R as substitution of H.
L-T-waves:
The backbone chains (B) of proteins may be regarded as a kind of L-waves, (assumed in fields of gravity), when unbound expressed as dipoles in terms of the electromagnetic force. Perhaps they preceded the evolution of the side chains (R), these implying a dimensional step to T-waves, characterizing electromagnetic waves.
(Cf. perhaps a hypothesis by Copley et al (2005) that ams may have been constructed at the inner OH-group of ribose between nucleotide pairs.)
(Total number of atoms without H = 512 - 288 = 224.)
Note that interval 800 - 512, also 288, may be connected with G1
+ C1 too.
7b. Z-division on atom kinds when 24 + 4 H are moved to the B-chains:
Z - B-chains as 960:
C: = 288
N + H (120) = 288...Sum 576, 3 x 192
O = 384 = 2 x 192
Z - R-chains as 800:
C = 480 = 512 - 32,
N + O + H (124) + 2 S = 320 = 288 + 32
A division 3/2 between C-skeleton and " substituents".
Z - total. R+B 1760:
C = 2 x 384 = 800 - 32
S = 32
N + O + H (244) = 960
8. Pyramids on the 2x2-chain:
Building figure pyramids (as Pascal's triangles) on the 2x2-chain
leads of unknown reasons to numbers from the ES-chain (-1 in some
of them). A couple of examples are shown in Fig. 40.
Fig 13-9: Pyramids
on 2x2-chain, 176, 384 and 158, 574:
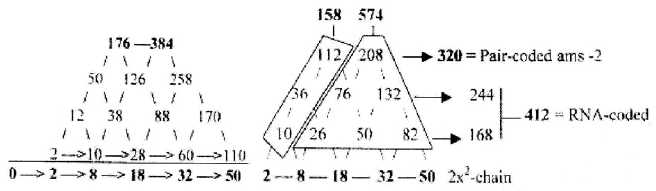
The left pyramid is built on the cumulative sum of the chain and
gives on level 3 the top numbers 176 and 385-1, interval 208, to
compare with the 770-group of ams as intervals in the ES-chain.
The right pyramid is built directly on the 2x2-chain
and shows the 734-group and its codon divisions when figures
are added in orthogonal directions, -1 in the G+C- and U+A-sums. 574 - 158, interval 416.
Note e. g. A1 = 497 = 176+1 in group 770 plus
320 in group 734 = 496 +1.
"2-base-coded" ams = 336-1 is the sum of 176 in
the 12-group 770 (GU+CU+UC+AC) and 158 + 1 in 12-group 734
(GG+GC+CC+CG). These numbers appear to the left, built from lowest
"dimension degrees" in the 2x2-.chain. (160
in figure 13-8 below).
Another way to see the right 574-pyramid above , 2 x 208 = 416, + 158 in accordance with the ES-chain. To the left the isolated 544-pyramid below.
Fig 13-10a, 10b::
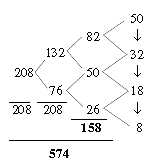
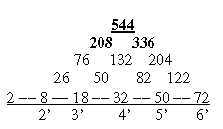
Extending the 2x2-chain with x = 6 - 0 in Fig. 41,(
top of pyramid to the right), and with an orbital 22 gives e. g.
the sums 292 for level 1, 460 on level 2, first sums
in the ES-chain, and sum 1638 on levels 0 to 4. half the
total of 24 unbound ams.
Fig 13-11: Pyramid
1638, the top of it to the right:
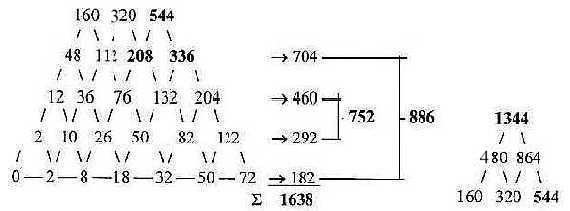
- 752 = ½ x R-chains, 886 = ½ x B-chains
of ams.
- On level 3 and 4 we get the numbers 336 - 208, sum 544.
- Top number becomes 1344, sum of 24 bound B-chains.
Do we have to count on a 6th dimension or rather rely on Einstein
that the relation between two bodies is 6-dimensional?! Only for
a total 544. Note: G+C 544 = 384 in left figure 13-7, the cumulative
pyramid, +1, + 160 - 1 in figure 13-8.
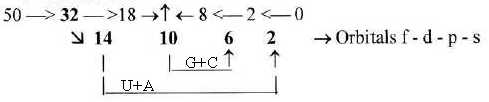
9. About 3rd-base groups of ams:
Number of ams in the G+C- and U+A-groups are possible to associate
to orbital numbers, as in figure 13-6 below. U+A: 14 ams, 2 with
indifferent 3rd base; G+C: 10 ams, 6 with indifferent 3rd base.
Fig 13-12: Codon
groups after 3rd base compared with orbital numbers:
A note:
Ams with 3rd base A/G (+ A or G) = 638
638 = 352 + 286 = 11 x 32 + 11 (18 + 8), orbital
numbers
Together with all "debranched " 2-base-coded ams 335
we get the sum = 973.
973 = figures 1/2 x (18 + 14 + 10),
-2.
3rd base U/C = 531
531 = 1/2 x figures 10 - 6 -
2.
10. Two more special annotations:
a) Numbers 110 and 26:
Two numbers in the 2x2-chain, 110 as the sum of the whole chain and 26 as the sum of middle two numbers 18 + 8, give associations to the displacements between single base groups of ams from 1st to 2nd base order: +/- 2 x 110 in the G- and C-groups and -/+ 26 in the U- and A-groups. An eventual connection?
I needs a two-way direction aspect on the G+C-groups versus one-way direction in the U+A-groups.
Compare the numbers in these differences:
To purine - pyrimidine group:s:
U+A = 960, – 26 = 934 = G2 + A2; from U + A, ~ U →
G
G+C = 544, + 26 = 570 = C2 +´U2; from C + G, ~ G → U
To keto- / amino groups:
U+A = 960, – 110 = 850 = C1 + A1; from U + A, ~ U → C
G+C = 544, + 110 = 654 = G1 + U1; from G + C, ~ C → U
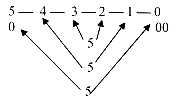
b) Some numbers of the 2x2-chain, orbitals, cumulative ones as 28 etc.
read in opposite directions:
28 + 82 = 110, x 2 = 220 = UG + GU
26 + 62 = 88, x 2 = 176
18 + 81 = 99, x 2 = 198 = CA + AC
14 + 41 = 55, x 2 = 110
10 + 01 = 11, x 2 = 22
08 + 80 = 88, x 2 = 176 = CU + UC + GU + AC
06 + 60 = 66, x 2 = 132 = GA, AG
02 + 20 = 22, x 2 = 44 (CO2)
*
To Halved orbital
numbers as a superposed chain.