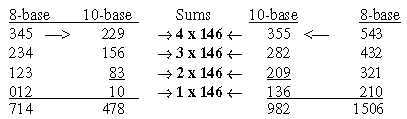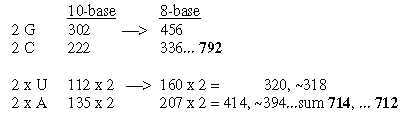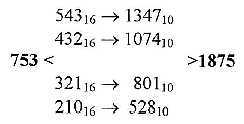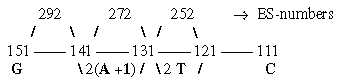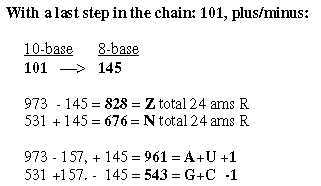I.  Triplet series; intervals outwards - inwards:

1.1  Triplet chains in nb-8, transformed to nb-10:

The triplets as 4 numbers in two series, outwards and inwards (as 543-345, 432-234 etc., treated as nb-8-numbers, give in pairs in nb-10 sums 4 x 146, 3 x 146, 2 x 146, 1 x 146, the total 5 times 292 =  5' in the ES-chain.
   Intervals in nb-10 "outwards - inwards" = 126, ½ x 252 ( 4').

Fig. 21-1:

982 = 2 x 491: 491-10→753-8   But 478-10 →736-8 .

Triplets read "inwards" approximate the 734-group of ams in middle of the ES-chain, hypothetically representing an inward direction in relation to the 770-group as outward directed.
   Cf. for 982 file 18, figure 18-3 and for directions file 14, para 3, figure 14-2.

Fig. 21-2: Number 982:

1.2   Codon bases read as nb-8-numbers give sums triplets in nb-10:

Fig. 21-3:

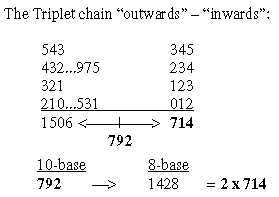
2. Sums 1506 - 714 and intervals 792:

Fig. 21-4:

Fig. 21-5: Total sum of R for 24 ams, sum 1506 -2 from 2 x 4 bases:

3.  Number n x 273 from codon bases;, two other transformations:

273, the mean value of 2 ams R+B unbound:

 nb-16       nb-10

C-base: 111    —> 273     

The triplet chain with intervals 111: 543 - 432 - 321 - 210:

210-10 → 546-6 = 2 x 273.

From file 20: Number n x 111, the intervals in the triplet steps:

Fig. 21-6:

4.  The triplet series and number 1875:

Pairs of the triplets = 753 transformed as a number in nb-16 gives 1875 in nb-10.
   All 4 triplets separately transformed, see figure below, give n x 273 as the differences.

Fig 21-7: Number 1875:

Intervals 1347 - 528 = 3 x 273 = 819, x 4 = 3276, total R+B of 24 ams.

The sums (pair wise added) reminds of the second spectral line of hydrogen from Balmer series, mentioned in Introduction: Formula 1/2² - 1/4² = 0,1875. Cf. 210 and spectral line 0,21 (!).
1/22 - 1/32 = 1/4 - 1/9 = 0,138888, the 3rd spectral line

Two other operations give relations between sums and intervals:

¹⁰log 1,875 ≈ 0,273 00...
187,5^2/3 x 100 = 3275,93 ≈ 3276, total of 24 ams R+B

[1/4 x ES-chain numbers = 73 - 63 - 52 - 39,75 - 25 ,
mith exponent 3/2 = 623,7. - 375. - 500. - 250,6. - 125 : um ~1875 (1874,32.]

Note 63 x 52 = 3276, total sum of 24 ams R+B. Cf. "quark-numbers".

15/8 = 5x3x1 / 4 x 2 = 1,875.
24 ams R+B = 3272, close to 8 x 409.
48 codon bases (1st and 2nd) = 6141, clooe to 15 x 409 (6135)
Real quotient 1,874542.

II.  An alternative numeral series

Another series, from G- to C-base:

Such a series, not treated above, shows some interesting features:

151 - 141 - 131 - 121 - 111

First and last numbers = mass of G- and C-bases. The DNA-bases (+1 in A-base) are shown in figure below: 272 = 2 x 136 (~ Hypoxanthine), 252 = 2 x 126 = T-base:

Fig 21-8: An alternative series G - to C:

With last three numbers doubled the sum in nb-10 = 2 x RNA-bases = 1018, in nb-8 = 1772, the 24 unbound B-chains.
   All these numbers transformed to nb-8 give the triplet sums 975 (543 + 432) - 2 and 531 (321 + 210), sum 1504, 24 ams R:

Fig. 21-9:

The 12-groups 770 and 734 of ams are shown in the figure below. Here it may be noted that we get the 734-group in the middle of the chain as in the ES-series, with 2 times 208 in that chain included, corresponding to both 203-groups here.

Fig 21-10:

The ams groups 816 and 688 from -/+ last number 157:

973 -  157 = 816 = U1 + C1
531 + 157 = 688 = G1 + A1.

Some other paired groups of ams R from this alternative series:

Fig. 21-11:

Fig. 21-12:

*