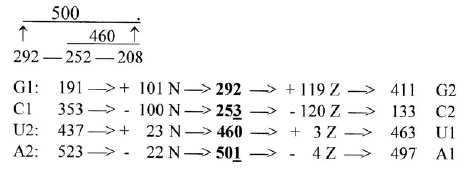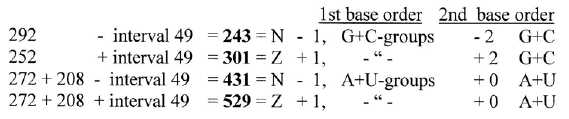Number 26 and total N and Z derived from the ES-chain:
Number of H-atoms is of course an essential result of and expression for structures of ams. Total N- and Z-sums without H = 2 x 676 = 2 x 26². (Cf. file 13, about the 2x^2-chain behind the periodic system: 26 as 18 + 8 in the middle of this chain and 26 as factor in total sum R+B of ams, 3276 = 26 x 126.)
   N-Z-sums derived from the ES-chain (?):

Z = 2 x 544 -  259 = 829, - 1 = 828,
N = 2 x 208 + 259 = 675, +1 = 676.

N-Z-division similar to division between codon groups of ams:
In Table 1 it could be noted that N- and Z-sums didn't change more than one single unit (u) between main groups G+C and U+A from 1st to 2nd base order (as if only through a change n → p!), indicting that also N-Z-divisions may be guided by the numeral series.
We had the same similarity among mixed and non-mixed codons:
    N-Z-division in 770-group shows up to be the same -/+1 as between Form- and Cross-coded ams: N = 2 x 176 - 1 = 351 and Z = 2 x 209 +1 = 419.
    In the the other 12-group 734 the same concerns the A-U-group: N = U1-coded ams +1, Z = A1-coded  ams -1.
    This is one among several examples of similar number divisions within different basis of mass divisions as along different coordinate axes.
    (Another example is e.g. the number of atoms in 48 codon bases, 1st and 2nd position, = 674 (2/3 x sum of the ES-chain 1011): See file 10 about the bases.

Displacements in N-Z from 1st to 2nd base order:
Dividing the differences - as "displacements" - between codon base groups in 1st and 2nd base order in N and Z gives as a border numbers of the ES-chain (+1 in C- and A-groups), shown in figure 7-1. A-groups = 500 = 3' + 5', U-groups = 460 = 4' + 3'. Cf. R-chains: A1 = 500 -3, U1 = 460 +3.

Fig 7-1: N-Z-border between 1st and 2nd base order:

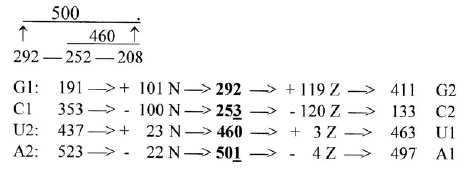
Note that the order U+A in the figure have been reversed, 2nd to 1st base order.
   U1 463 -  3 Z = 460, -  23 N = 437 = U2     
   A1 497 + 4 Z = 501, + 22 N = 523 =A2   
Adding displacements of pyrimidine and purine bases respectively, we find that they are exactly the same in N and Z = 123:

C1 + U1 →  C2 + U2 = -  123 N, - 123 Z.
G1 + A1 → G2 + A2 = + 123 N, + 123 Z

U-C-pair is divided in step 1 - 2: 100 - 23 (+/-1): 1 —|—2 ——  3
A-G-pair is divided in step 2 - 3: 120 -   3 (-/+1): 1 ——2 —|— 3

Displacements 220 and 26,:in G-C-groups 220, in A-U-groups 26.
Cf. a series 102 - 82 - 62 - 42 - 22: (Series = 2 x the 2x2-chain, see file 13.)

100 - 64 - 36 - 16 - 4: Sum 220
  N            Z

1/2 x (36 + 16) = 26, n+Z-displacements in the U-A-group in the middle

Another way to get these numbers, abbreviated:

G-C: 5^4/3 - 4^4/3 , x 100 = 220. A-U: (5+3)^4/3 - (4+3)^4/3, x 10 = 26.
Could the exponent 4/3 represent an underlying level?

 

√3/2:
√3/2 gives the total relation Z - N = 828/676 very closely, as it does in the separate G+C- and U+A-groups.
   The number of H in these main groups is circa 1/10 of totals 544 and 960, 55+/-1 in G+C-groups, 97 -/+1 in U+A-groups.

Interval 49 in the middle step: 3' - 2'
The interval in step 3' - 2' (208 - 159) at the middle of the ES-chain = 49. Divisions of sums 544 and 960 -/+ 49 (+/-1) give approximately the N-Z-division between main codon groups G+C, A+U:

Fig 7-2: N-Z-division approximately from -/+ middle interval 49:

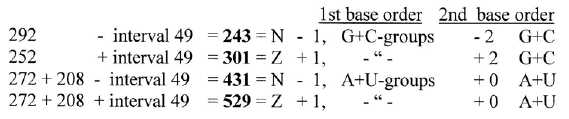
Here we could associate to a d-degree step 3 - 2 as a relation mass versus charge: neutrons n polarized by weak interaction into charges, protons and electrons:
   n → p+ + e- + antineutrino. (H2PO4- = 49 z)

H-atoms:
Total number of H-atoms in 24 ams R-chains = 152 = 8 x 19.
It is rather precisely distributed on the individual codon groups as 1/8 - 2/8 in G-C-groups, 2/8 - 3/8 in U-A-groups with exchange of the numbers from 1st to 2nd base sums:

   G1 1/8, C1 2/8, G2 2/8, C1 1/8.    U1 2/8, A1 3/8, U2 3/8, A2 2/8.

This makes it possible to derive the N- and Z-numbers of the individual codon base groups -/+ 1-2 units. Examples:

G1 = 191 A, - 19 = 172, x ½ = 86 = N, + 19 = 105 = Z
A1 = 497 A, - 57 = 440, x ½ = 220 = N+1, + 57 = 277 = Z -1.

A special observation regarding 3rd base groups:

The figure shows ams with differentiating 3rd base, to the left from glycolysis, to the right from the citrate cycle.

Fig. 17 files, 02-10 a, b:

 

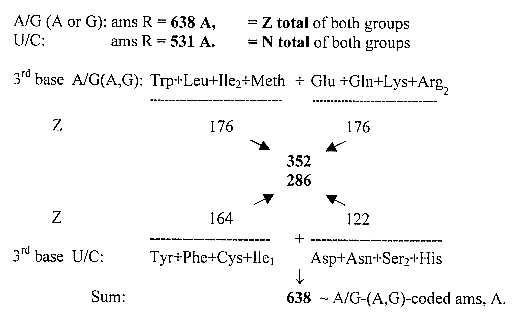
This is still another example of equal number divisions along different "property axes".

(In numbers of the ES-chain:
     272 + 367 = 638 +1. 272 + 259 = 531
or 584 +/- 54, half the interval 3'- 1' 108 = 531 -1 and 638.)

*

To Geometries, Golden section and special arithmetical operations.