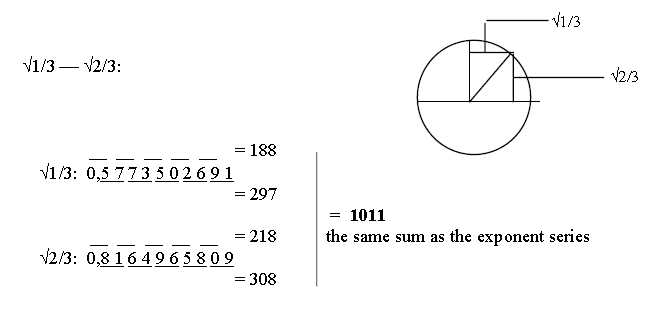Hopefully some advanced mathematicians will find
this file on the web and get provoked enough to search for explanations!
Geometrical relations in the two 12-groups:
385 x √2 is ~ 544. Through this factor √2 and
inversions (/\ ) the codon groups 385 and 367 in
the ES-series become related, figure 8-1 below.. How to interpret
such relations? They are very likely only one example among many
similar dimensional relations on a deeper underlying level that
remains to investigate. (√2 should probably not be
regarded as a relation diagonal/side in a square, sooner
in its serial development?)
Fig 8-1: Geometrical relations through √2:
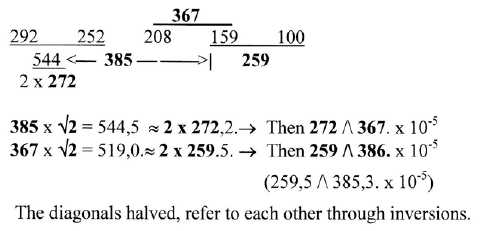
Two notes:
1) A right-angled triangle with the sides 176 and 209 (the number
division of 385 within mixed codon groups) gives the hypotenuse
273.23.; 273 the mean number of two ams R + B unbound.
2) Cf peraps the relations between Z-numbers of ATP and NADPH(+H)
around 258 - 387, a 2/3-relation, 6 x 43 --- 9 x 43. see
Biochemistry.
Intervals in the ES-chain with exponents 3/2 and 4/3:
Intervals 40-44-84 in the ES-chain with exponent 3/2 gives numbers
253 292, and 770, as a kind of feed back (?) or mutual references
, re-establishing the ES-numbers 5' and 4' (+1):
403/2 = 252.98.
= 253.
443/2 = 291.86. =
292. ........Sum 544 +1.
(Third number 208?: 84 - 49 = 35, → 353/2
= 207.06. = 208 -1)
843/2 = [292 - 208]3/2
= 770. = Cross- plus Form-coded ams.
Compare with 42, 1/2 times the interval 84, divided and whole
number:
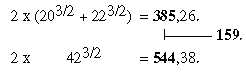 Fig. 8-1-b
Fig. 8-1-b
Intervals in the three middle steps of the ES-chain, sum 152:
443/2 = 291.9.
493/2 = 343
593/2 = 453.2.......sum 1088.15.
= 2 x 544.
|
Exponent 4/3 ?
Testing this exponent - as related to a higher d-degree step 4
- 3 (?) - shows up to be another way to re-establish the starting
number 292:
404/3 + 444/3
→ 292.13. (Cf. 52/3
= 2.924.)
Note that 404/3 is about 136 +1
and 444/3 about 156 -1: 136 mass of Hypxanthine, 156
mass of Orotate, the parents of the bases in the codons
844/3 = 367.9.
= 208 + 159, +1; x 2 = 736. = RNA- + Pair-coded
ams +2.
The golden section:
The golden section (gs) as Fibonacci series appears also in this
ES-chain and mass relations within groups of ams. Following series,
figure 8-2, leads from 2' in the ES-series to total sum R + B
of the 24 bound ams through steps as times gs:
The ES-numbers 208 and 367 gives for instance
the groups G+C 544 and U+A 960 approximately.
Fig 8-2: Golden section (gs) steps in the ES-series:

Higher numbers abridged. Number 257. = 208 + middle
interval 49. In 7th step we get 2848, x gs = 2 x 2304 = 2 x
482.(24 = number of codons, ams.)
Forms of R-chains:
Elementary structure of R-chains as basis for grouping of ams
may give three elementary groups: vary roughly ring-formed, "straight"
and "branched":
Ring-formed ams 292 + 159 (a loop 5' - 2'.) = 451,
three aromatic ams 328, + His + Pro 123.
"Straight" ams = 2 x 159 (2') = 318,
Ala, 2 Ser, Thr, Cys, Lys, Meth = 317, + Gly 1.
Ring-formed + "straight" = 770
-1.
Branched = 734 +1 (as at middle of the ES-chain):
CHx-groups = 271; O-OH + O-NHx = 262; 2 Arg NHx-NHx = 202.
π and √2 , an arithmetical curiosity:
Reading and adding 2 x 5 two-figure-numbers (31 + 41 + 59...,
14 + 15 + 92...) from first eleven figures in these transcendent
celebrities gives both whole and partial sums of the codon grouped
amino acids as well as vertically numbers from the exponent series,
see the figure below.
No motivation for the operation is offered here.
Should there exist any sense in the operation, it's left to more
advanced mathematicians to find it.
Fig 8-3: π and √2:

*Cf. fig.
4-1.
Sums of numbers from π = 431 and from √2
= 321; cf. triplet
numbers 432-321.
A note:
If √2 is seen connected to d-degree step 2-1
and π to step 3-2, the number 321 from √2
could be thought of as displaced, here one 10-power step:
Fig. 8-3-x. Sum 431 + 321 with displaced
321 number
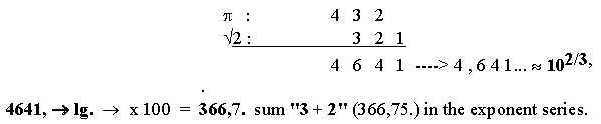
[Cheops pyramid:
½ x 292 = 146 ~ the height of this
pyramid - in meters!
½ x 460 = 230 ~ side of this pyramid
- in meters!
If the old Egyptians were acquainted with cubic roots and exponents
2/3 is probably uncertain. The Pharaoh measure "ell" is
said to have been about half a meter.
That the circumference of the base is approximately
2π times its height is a well-known fact.
460/292, x 2 = 3.15068, differs from π 3.1415... with ~ 3 pro
mille.
π and √ 2 in figure 8-3: the
2-figure numbers summed in another way:
One example:
π 31 14 41 15
59 92 26 65 53 35
√ 2 14 41 14 42
21 13 35 56 62 23
210+2
367
175-2
|
|
385
[212 x 173 = 366,76 x 10^2. 3' + 2' = 366,74.)
What kind of relation could exist, which closely couples π
and √ 2?
π represents 1/2 of a unity circle, but √
2 only 1/4, if illustrated as in the figure
below? Could we interpret it in terms of a step or displacement
in dimension
degree 3 to 2: (4-3-1 → 3-2-1 as sums of the 2-figure numbers
above)? π related to a 3-dimensional world, √
2 to a 2-dimensional one.
Fig. 8-4 Bell's theorem
a.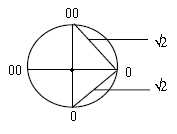 b.
b. 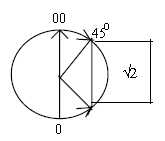
Assuming the definition of a dimension as characterized by two
complementary “end-poles” (0 - 00 in figure a), the
shortest step between the poles in an 1-dimensional world would
be 2 r and the shortest step in a 2-dimensisonal world could be
only √2. In a 3-dimensional world, the shortest
way could be the circular one (with reference to Einstein)?
(There is an association here to Bell's theorem and Aspect's experiments
with photons in quantum physics: measurements in two dimensions
(directions) as φ a branched way for two possible outcomes.
If there were no coupling between the photons, the maximum result
of Bell’s formula should be +/- 2. But the experiments
showed on a maximum of +/- 2√2
showing that the photons were entangled.
The question arises: what would be the result
if such measurements were carried out in three dimensions?)
√2 representing the
tangent of an angle, a direction?
Arc tan √2 = φ 54.736.
Sin φ = √2/3,
Cos φ = √1/3
Treating these numbers sin - cos in the same way as π
and √2 above gives these results:
Fig. 8-5. Sin - Cos for arc tan √2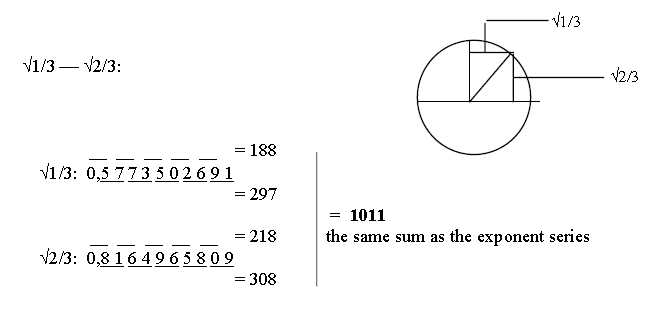
Taking each other 2-figure number from the cosine
series and each other from sine numbers, the upper ten first,
gives sums of the ES-chain:
Fig. 8-6. Sin-Cos-series with sum 1011 of
the ES-series

*
To Glycolysis
- Citrate cycle.
|
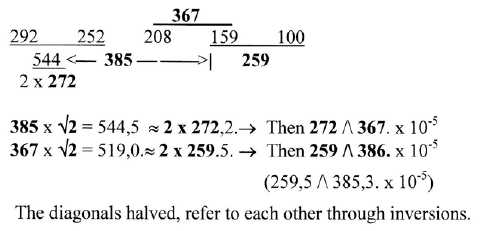
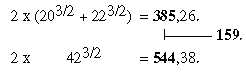 Fig. 8-1-b
Fig. 8-1-b

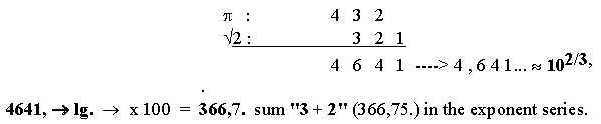
 b.
b.