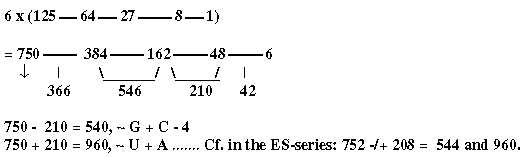1. Middle numbers 27 and 8:
In an x3-series, (x = 5 - 0), the numbers 27 and 8 appear around the middle step 3 - 2. They are the factors in the astonishing regular table of ams with mixed codons (file I-02 here) where the ams with differentiating 3rd base in their codons amount to 594.
An x3-chain and factor 35 in the 12-group 770:
33 23
125 — 64 — 27 —- (19 ) — 8 —
1 — 0. (x = 5 - 0)
Table I-2:
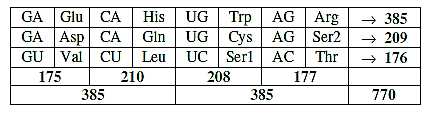
Sums of rows in the table:
385: 27 + 8 = 35, →, x 11 = 385
209: 27 - 8 = 19; → x 11 = 209... Sum 594 = 27 x 11 x 2.
176: = 8 → x 11 x 2
One 27 number disintegrates into interval 19 and 8 into rows two and three..
(The factor 11 in this group of ams with mixed codons gets no special explanation in this x3-chain.)
A note:
About factor 11 among ams with mixed codons as an expression for double-direction in steps (file I-05): 01 + 10 = 11, the last step in the elementary chain 5-0. Cf. steps in the half orbital chain 9-7-5-3-1 read as 97 - 75 - 53 - 31 = - 2 x 11 in each step.
(Are there eventually any 11-factor in quark computers?)
Compare also the atomic mass of bases A and U and interval 27 - 8 = 19 divided 5 - 14, (interval 9 as in a simple reading of the step in opposite directions 32 - 23)
A-base 5 x 27 = 135, U-base 14 x 8 = 112
Cf. these numbers 112 and 135 from quotients between spectral lines of hydrogen (end of Introduction
About some other numbers in the x3-chain compared with the ES-chain, see below.
2. A root in physics of number 544?
Numbers 27 and 8 have appeared in group theories
of elementary particle physics (Gell-Mann M in The Eightfold Way 1964)), this mentioned with
nothing of a closer knowledge in that field.
A suggested connection here seems supported by following relations in figure 16-1 below, which could imply that number 544 for the G+C-group of ams had its root in the the mass quotient between the electron (e) and the proton (p) of a single H-atom - or rather (e + p) / e ≈ 1837.117 x10-6.*
* p/e ≈ 1836.12, /\ = 544,623 x 10-6. If p/e = 975 x 103 / 531 (a quotient in the middle in the chain of halved orbital numbers = 1836.158, the inverse becomes 544.615 x10-6.
(Two similar or equivalent numbers may of course have very different origins as similar words in languages. Cf. [7/3]2 = 544,444, /\ 1837,34 x 10x and chapter 1/ 7 in Bichemistry.) )
The square root of 8/27, x 10-3 = [2/3]3/2 = 544.331... x 10-3 is a similar number, however not exactly the same.
A suggested connection here seems supported by
following relations in figure 16-1 below, which could imply that
number 544 for G+C-group of ams may have its root in the p/e-quotient
of a single H-atom:
Fig 16-1: Square roots of 27/8, and inversions of 27 and 8:

1/4 of the period 296 = 2/27 = 740740740... (x10x)
is the inversion of A-base number 135.
Inversions may be regarded as one kind of references between units
or energy levels in complementary fields outside - inside number 1 as a ring around the origin in a coordinate system.
The numbers 1836 and 544 among ams as quotients,
however, concern units on different levels, referring to number
of e and number of u (~ shell versus nucleus in the atom). If we
could assume that quotients as such reappear on different levels,
already a single H-atom in some way could include resonances in
the future development of life.
More reasonably expressed, the same underlying
elementary number series in its development gives such number relations
on different levels through the evolution.
A bit curiously the "same" number 544,33..as from √8/27 is given out of a "factor chain", 1 to 5 times 2-figure numbers of steps in the elementary chain:
(8/27 → √ = 544,3310540 x 10-3, → √ = 1,837117307.)
A "factor chain:"
1 x 54
2 x 43
3 x 32
4 x 21
+5 x 10 ---> 54 86 96 84 50 → √ = 74074,074074... → √ = 272,165...
= 370
5 x 74 x 2 = 544,3310540*
*The numbers differ after the 11th digit!
( A factor chain in opposite direction, 1 x 45, 2 x 34 etc.. gives the sum 5 x 47, the factor in total ams R 1504 and the mass of Cys.)
To summarize, the numbers 27 and 8 may through simple operations join approximate numbers the inverted p/e-quotient , the masses structuring ams masses (R) of mixed codons, the sum 544 of G1 + C1 and its division on these codon groups and the A-base with its inversion of a periodic 74, the mass of unbound B-chains of ams..
If the numbers 27 and 8 in group theory for elementary particles has been connected with the e/p-quotient is left unknown here. Perhaps it is two different hypothesis that are involved in the figure above for the origin of the number 544?
The number 385 gets its simple explanation directly from 27 and 8, apart from factor 11, and 544 was shown as ≈ √2 times 385, through inversions and halving connected with approximate number 367, the sum of the 12-group of ams with non-mixed codons (in file I-8, fig 8-1).
The e/p-quotient, or e/(e+p) as a deeper root for number 544 seems to concern a more fundamental issue about inversions and conjugates in higher dimensions; inversions as a property of steps towards higher levels of complexity and the biochemistry of life.
Cells are in some respects the inversions of an atom, especially in the relation of charges, with dominating negative charge inside, mostly carried by the proteins, and positive charge outside. The hydrophobic bonds in P-lipids of cell membranes could be imagined as one expression for an inversion (center to anti-center) of the strong force (Fst) on this higher level. (The mentioned group theories are also used in analysis of the electroweak and strong forces.)
3. Some numbers in the x3-chain times 3 compared with the ES-chain:
Besides the middle numbers 27 and 8 here, the x3-chain as a whole doesn't any simple correlations with elementary codon groups of ams in similar ways as in the x4, x1 and x2-chains (files II: 13, 15, 16).
Some numbers could or should eventually be noted. With a factor 3 times the series we have 375 - 192 - 81 as first three numbers:
- 375 =1/2 x 750, 1/8 of a total sum 1500, approximating the total of R of 24 ams.
- 192 is a returning factor in 385-1, 770 -2, 575 +1 (the U+A-group in 12-group 734), in
960 (U+A-groups R) and in 1344 (sum of bound B-chains)
- 81, 3rd number in the x4-chain (file 15).
- 192 + 81 = 273, the mean value of 2 unbound B-chains.
- Interval 111, (cf. reference Scherbak) is the number for steps in the triplet series x1
(file 15). (111 in a hexagonal system = 273 in a decimal system.)
6 (3 x 2 in step 3 - 2?) times the x3-chain gives a series that have some similarities with the ES-series:
Fig. 16-2:
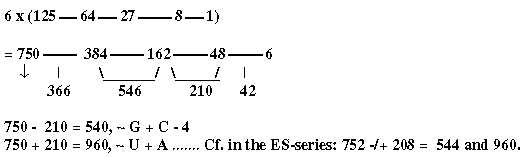
- 750 divided in ams with mixed (385) - non-mixed (367) codons (the first interval here), -1 in each group.
- 162 ~the difference G1 - C1.
- 384 + 162 =385 + 159 + 2 = 546, 2 x 273, (4' + 3').
the mean value of 2 unbound ams.
- 384 + 210 = 4' + 3' + 2' in this chain = 594 = 385 + 209 in the table above
- Interval 4' - 2' = 384 - 48 = 336, 6 B-chains bound.
The sum of the whole series 225 times 6 = 1350.
1350 → √ = 367.42 x10-1, → /\ =272.1655 x10-4 , x 2 = 544.331054 . 10-4 =
= 1/10 of √8/27.
However, if there is a deeper relation between the factors 27 and 8 here and the ES-chain remains an open question. It is possible that these numbers should not be associated with a whole x3-series at all but represent a transformation of exponents in step 3 → ← 2 of the ES-chain, with the background model (fig 03) in mind
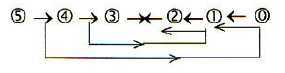
and the double-directed processes, meeting in the middle step, somehow implying a change of the exponent 2/3 to 3/2 and including an inversion... Cf. the assumption in the background model of new levels developing through step 3 → ← 2.
x4 → 3x3 → x3/2 → ↑↑← x2/3 ← 2x2 ← x1
There is a similar pattern of two-way direction in the protein synthesis, where tRNAs as from opposite strands of DNA meet mRNA "the other way around" at ribosomes in the "middle" of the process.
Number of codons:
This x3-chain as basis for number of codons?
- 5 bases T/U-A-G-C become
- 4 inwards DNA and 4 outwards in RNA, which, become.
- 3 bases in codons, as 3 positions on ribosomes. Third position
indifferent gives
- 2 bases relevant in one 3rd of codons. Then leads to
- 1 base in nucleotides, becoming active coenzymes in–MP, -DP, -Taprooms.
4 bases gives 64 possible codons but leads to
3 bases in actual codons = 27 differentiating ones including 3 stop codons,
2 bases relevant in 8 codons.
Rest 19, 27 - 8 codons with more or less halfway defined
3rd base in step 3 - 2:
- 8 ams with 3rd base U/C,
- 8 ams with A/G, A or G, (5 A/G-coded, 3 ams "3-base-coded"),
- plus 3, usually stop codons (or 2 if we count UA-A/G as one).
We could possibly imagine that it's the interval
step 5' → 4' = 61 (125 - 64)
that decides this reduction and appears in later numbers as potential
"pre-codons" ?
(With this view it's possible to imagine that the not ams coding parts of DNA-strands, should be divided in quadruplets for the interpretation? Cf. perhaps how strands are cut, giving sticky ends?)
Number of codons as halvings:
64 → 32: 32 = "2-base-coded", x 4: 8 ams = 335
32 → 16: 16 = U/C-coded, x 2: 8 ams = 531
16 → 8: A/G-coded, x 2: 5 ams = 376, + 3 ams x 1, A or G = 262
+ 3x1, usually stop codons
*
To Section III: Transformations
between number-base systems